Dalam statistika, regresi linier adalah sebuah pendekatan untuk memodelkan hubungan antara variabel terika Y dan satu atau lebih variabel beas yang disebut X. Salah satu kegunaan dari regresi linier adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya Contoh yang dibahas kali ini adalah mengenai penentuan penerimaan pengajuan kredit sepeda motor baru berdasarkan kelompok data yang sudah ada.
Ada beberapa cara menyelesaikan permasalahan regresi linier, salah satunya adalah melalui teknik Dekomposisi Eigen. Teknik ini mendekomposisi sebuah matriks A menjadi 2 matriks V dan D. V adalah matriks persegi yang masing-masing kolomnya berisi eigenvector, dan D adalah matriks persegi dengan nilai pada elemen diagonal adalah merupakan eigenvalue dari masing-masing baris data.
Diasumsikan ada 3 tipe motor yang sudah diketahui datanya, yaitu Motor A,B,C
Masing-masing tipe motor memiliki kriteria, yaitu harga, jarak tempuh per liter, cc, dan memiliki hasil jual dalam unit
Diasumsikan data dari 4 tipe motor tersebut adalah sebagai berikut:
| Motor | Harga | Jarak tempuh per liter | cc | Unit Terjual |
|---|---|---|---|---|
| Motor A | 10.000.000 | 35 | 110 | 20 |
| Motor B | 11.000.000 | 40 | 150 | 12 |
| Motor C | 14.000.000 | 37.5 | 125 | 17 |
Contoh data awal adalah sebagai berikut:
Dim dataSisiKiri As Double()() = {New Double() {10000000, 35, 110}, _
New Double() {11000000, 40, 150}, _
New Double() {14000000, 37.5, 125}}
Dim dataSisiKanan As Double()() = {New Double() {20}, _
New Double() {12}, _
New Double() {17}}
Selanjutnya ada 4 buah motor lagi, yaitu E,F,G,H, yang baru akan diluncurkan, sehingga tidak diketahui hasil jualnya
Maka tentukan data-data ini nantinya diperkirakan memiliki hasil jual berapa unit
Diasumsikan data awalnya adalah sebagai berikut:
| Motor | Harga | Jarak tempuh per liter | cc |
|---|---|---|---|
| Motor E | 13.000.000 | 45 | 125 |
| Motor F | 12.000.000 | 47 | 110 |
| Motor G | 10.500.000 | 43 | 110 |
| Motor H | 13.500.000 | 35 | 125 |
Contoh data baru adalah sebagai berikut:
Dim dataBaru As Double()() = {New Double() {13000000, 45, 125}, _
New Double() {12000000, 47, 110}, _
New Double() {10500000, 43, 110}, _
New Double() {13500000, 35, 125}}
Langkah-langkah penggunaan algoritma ini adalah
* Catat matriks persamaan sisi kiri pada layar
Dim A As New ObyekMatriks(dataSisiKiri)
* Catat matriks persamaan sisi kanan pada layar
Dim b As New ObyekMatriks(dataSisiKanan)
1. Lakukan proses dekomposisi matriks menggunakan metode dekomposisi Eigen
Dim eigen As EigenDecomposition = A.EigenD
* Skrip tersebut akan melakukan inisialisasi pada Class EigenDecomposition. Class ini berisi tentang variabel dan fungsi-fungsi yang digunakan untuk melakukan dekomposisi. Deklarasi Class EigenDecomposition adalah sebagai berikut:
Public Class EigenDecomposition
Private ukuranMatriks As Integer
Private isSimetris As Boolean
Private m_d As Double(), e As Double() 'Matriks untuk menyimpan eigenvalue (real dan imajiner)
Private V As Double()() 'Matriks untuk menyimpan eigenvector
Private H As Double()() 'Matriks untuk menyimpan bentuk nonsimetris Hessenberg
Private ort As Double() 'Matriks untuk menyimpan perhitungan algoritma ukuran matriks tidak simetris
. . .
Public Sub New(Arg As ObyekMatriks)
Dim A As Double()() = Arg.GetArray
ukuranMatriks = Arg.GetUkuranKolom
V = New Double(ukuranMatriks - 1)() {}
For i As Integer = 0 To ukuranMatriks - 1
V(i) = New Double(ukuranMatriks - 1) {}
Next
m_d = New Double(ukuranMatriks - 1) {}
e = New Double(ukuranMatriks - 1) {}
isSimetris = True
Dim j As Integer = 0
While (j < ukuranMatriks) And isSimetris
Dim i As Integer = 0
While (i < ukuranMatriks) And isSimetris
isSimetris = (A(i)(j) = A(j)(i))
i += 1
End While
j += 1
End While
If isSimetris Then
For i As Integer = 0 To ukuranMatriks - 1
For j1 As Integer = 0 To ukuranMatriks - 1
V(i)(j1) = A(i)(j1)
Next
Next
'Proses mendapatkan tridiagonal
tred2()
'Proses mendapatkan diagonal
tql2()
Else
H = New Double(ukuranMatriks - 1)() {}
For i2 As Integer = 0 To ukuranMatriks - 1
H(i2) = New Double(ukuranMatriks - 1) {}
Next
ort = New Double(ukuranMatriks - 1) {}
For j1 As Integer = 0 To ukuranMatriks - 1
For i As Integer = 0 To ukuranMatriks - 1
H(i)(j1) = A(i)(j1)
Next
Next
' Lakukan reduksi menjadi bentuk Hessenberg
orthes()
' Lakukan reduksi bentuk Hessenberg menjadi bentuk real Schur
hqr2()
End If
End Sub
. . .
End Class
2. Dapatkan matriks eigenvector (V) dari proses dekomposisi tersebut
Dim V As ObyekMatriks = eigen.GetV
3. Dapatkan matriks D dari proses dekomposisi tersebut
D adalah matriks berukuran sama dengan matriks eigenvector dan nilai diagonal matriks tersebut berisi eigenvalue yang ada
Dim D As ObyekMatriks = eigen.D
4. Lakukan rekonstruksi matriks A dengan rumus:
A = V * D * Inv(V)
Dim hasil As ObyekMatriks = V.PerkalianMatriks(D).PerkalianMatriks(V.Inverse)
5. Hitung koefisien dari masing-masing kolom yang ada
Dim X As ObyekMatriks = A.HitungPenyelesaian(b)
* Lakukan proses penyelesaian persamaan linier A * X = B
Hasil pengembalian nilai fungsi adalah matriks X, sehingga L * U * X = B(piv,:)
Public Overridable Function HitungPenyelesaian(B As ObyekMatriks) As ObyekMatriks
If B.GetUkuranBaris <> ukuranBaris Then
Throw New ArgumentException("Ukuran baris matriks harus sama.")
End If
If Not Me.IsNonSingular Then
Throw New SystemException("Matriks harus singular.")
End If
'Salin array B sebagai array hasil output persamaan beserta vektor pivot
Dim nx As Integer = B.GetUkuranKolom
Dim Xmat As ObyekMatriks = B.GetMatriks(vektorPivot, 0, nx - 1)
Dim X As Double()() = Xmat.GetArray
' Hitung L * Y = B(piv,:)
For k As Integer = 0 To ukuranKolom - 1
For i As Integer = k + 1 To ukuranKolom - 1
For j As Integer = 0 To nx - 1
X(i)(j) -= X(k)(j) * LU(i)(k)
Next
Next
Next
' Hitung U * X = Y;
For k As Integer = ukuranKolom - 1 To 0 Step -1
For j As Integer = 0 To nx - 1
X(k)(j) /= LU(k)(k)
Next
For i As Integer = 0 To k - 1
For j As Integer = 0 To nx - 1
X(i)(j) -= X(k)(j) * LU(i)(k)
Next
Next
Next
Return Xmat
End Function
6. Lakukan perhitungan dari masing-masing data awal menggunakan matriks koefisien X yang sudah ditemukan
Kemudian catat tingkat kecocokan perhitungan data dengan hasil awal pada data, untuk membandingkan apakah nilai X sudah cocok pada contoh data
Dim jumlahBenar As Integer = 0, jumlahSalah As Integer = 0
For i As Integer = 0 To dataSisiKiri.Length - 1
Console.Write("Motor " & Chr(i + 65) & " ")
Console.Write(dataSisiKiri(i)(0).ToString("N0").PadRight(11) & " ")
Console.Write(dataSisiKiri(i)(1).ToString.PadRight(23) & " ")
Console.Write(dataSisiKiri(i)(2).ToString.PadRight(4) & " ")
Dim y As Double = HitungUnitTerjual(dataSisiKiri(i), X.GetArray)
Console.Write(y.ToString("F0").PadRight(23))
If Math.Round(y) = dataSisiKanan(i)(0) Then
jumlahBenar += 1
Console.Write("Benar" & vbCrLf)
Else
jumlahSalah += 1
Console.Write("Salah" & vbCrLf)
End If
Next
Console.WriteLine("Jumlah perhitungan benar = " & jumlahBenar & ", jumlah perhitungan salah = " & jumlahSalah)
Console.WriteLine("Tingkat kecocokan perhitungan dengan hasil data adalah " & (jumlahBenar / (jumlahBenar + jumlahSalah)).ToString("F4"))
* Gunakan fungsi ini untuk menghitung hasil persamaan linier untuk data yang baru
Public Function HitungUnitTerjual(ByVal data() As Double, X()() As Double) As Double Dim hasil As Double = 0 For i As Integer = 0 To data.Length - 1 hasil += data(i) * X(i)(0) Next Return hasil End Function
7. Untuk masing-masing data baru, hitung perkiraan hasil unit terjual menggunakan koefisien beta yang sudah ditentukan
For i As Integer = 0 To dataBaru.Length - 1
Console.Write("Motor " & Chr(i + 65 + 4) & " ")
Console.Write(dataBaru(i)(0).ToString("N0").PadRight(11) & " ")
Console.Write(dataBaru(i)(1).ToString.PadRight(23) & " ")
Console.Write(dataBaru(i)(2).ToString.PadRight(4) & " ")
Dim y As Double = HitungUnitTerjual(dataBaru(i), X.GetArray)
Console.Write(y.ToString("F0") & vbCrLf)
Next
Hasil akhir adalah: (klik untuk perbesar gambar)
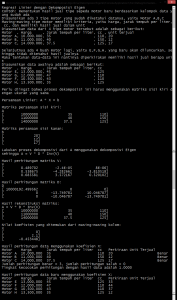
Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:
[sdm_download id=”3135″ fancy=”0″]
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.

Bisakah saya download modul diatas. Tetapi waktu saya download muncul pesan
Modul diatas sudah saya coba untuk download dan masih bisa diambil tanpa ada masalah.