Algoritma Dijkstra adalah salah satu algoritma yang digunakan untuk pencarian jalur. Contoh yang dibahas kali ini adalah mengenai pencarian jalur terpendek dengan biaya terendah.
Diasumsikan ada sebaran titik titik beraturan dalam sebuah grafik
Tidak semua titik terhubung satu sama lain, melainkan hanya melalui jalur-jalur tertentu saja
Dan setiap jalur memiliki biaya sendiri-sendiri
Tentukan Jalur yang harus diambil dari titik awal ke titik tujuan melalui jalur-jalur tertentu dengan biaya terendah
Dalam kasus ini, diasumsikan hanya ada 5×5 = 25 titik, dengan jalur sbb
| Titik Awal | Titik Tujuan | Biaya |
|---|---|---|
| 1 | 2 | 7 |
| 1 | 3 | 14 |
| 1 | 4 | 9 |
| 2 | 3 | 10 |
| 2 | 5 | 15 |
| 3 | 4 | 2 |
| 3 | 5 | 11 |
| 4 | 2 | 9 |
| 4 | 5 | 6 |
| 5 | 1 | 6 |
Langkah pertama adalah memasukkan data-data yang digunakan.
Contoh data adalah sebagai berikut
BiayaJalur(1, 2) = 7 BiayaJalur(1, 3) = 14 BiayaJalur(1, 4) = 9 BiayaJalur(2, 3) = 10 BiayaJalur(2, 5) = 15 BiayaJalur(3, 4) = 2 BiayaJalur(3, 5) = 11 BiayaJalur(4, 2) = 9 BiayaJalur(4, 5) = 6 BiayaJalur(5, 1) = 6
Jika diilustrasikan dalam gambar, maka model data awal adalah sebagai berikut
Sebelum masuk kedalam langkah-langkah pembahasan algoritma, ada beberapa konstanta atau parameter yang harus diketahui, yaitu:
* Tentukan jumlah titik yang digunakan
Diasumsikan dalam kasus ini, akan digunakan 5 titik dengan data jalur yang telah tersedia
Const jumlahTitik As Integer = 5
Langkah-langkah penggunaan algoritma ini adalah
1. Tentukan Titik Awal dan Titik Tujuan
Console.WriteLine("")
Console.WriteLine("Masukkan titik awal (1-5): ")
Dim awal As Integer = Console.ReadLine
Console.WriteLine("Masukkan titik tujuan (1-5): ")
Dim tujuan As Integer = Console.ReadLine
2. Lakukan proses perhitungan dengan metode Dijkstra dengan inputan titik awal
Penjelasan lebih lanjut tentang fungsi tersebut akan dijelaskan pada perhitungan dibawah ini (poin 2a – 2c)
For iAwal As Integer = 0 To jumlahTitik - 1 If iAwal = awal Then Dijkstra(jumlahTitik, iAwal) . . .
Memasuki perhitungan pada fungsi Dijkstra
2a. Inisialisasi Array Jarak ke titik lain
Pada array tersebut, selain indeks titik awal, beri nilai jarak dengan angka yang sangat besar
For j As Integer = 0 To jumlahTitik - 1 JarakKeTItikLain(j) = Infinity Next j JarakKeTItikLain(idxTitikAwal) = 0
2b. Inisialisasi Array Titik Terpilih menjadi benar semua, artinya semua titik tersedia untuk dihitung
Kemudian beri nilai array Jalur Sebelumnya menjadi -1
For j As Integer = 0 To jumlahTitik - 1 TitikTerpilih(j) = True JalurSebelumnya(j) = -1 Next j
2c. Lakukan perhitungan selama masih ada titik yang belum dihitung (poin 2c1 – 2c7)
Do While True . . .
2c1. Beri nilai awal jarak dengan nilai yang sangat besar
jarak = Infinity
2c2. Untuk masing-masing titik yang sudah terpilih,
Hitung jarak terpendek ke titik lain, dan simpan indeks titik dengan jarak terpendek
For i As Integer = 0 To jumlahTitik - 1 If TitikTerpilih(i) Then If JarakKeTItikLain(i) < jarak Then jarak = JarakKeTItikLain(i) u = i End If End If Next i
2c3. Jika nilai jarak tidak ditemukan, maka perhitungan selesai karena tidak ada titik lain yang menghasilkan jarak lebih pendek
If jarak = Infinity Then Exit Do
2c4. Beri nilai false untuk titik terpilih agar tidak dihitung pada perulangan berikutnya
TitikTerpilih(u) = False
2c5. Cari semua titik tujuan dari indeks titik yang terpilih (indeks u)
Lakukan perhitungan berikutnya apabila titik tujuan tersebut sudah terpilih dan terdapat jarak yang sah antara titik u dan titik tujuan
For j As Integer = 0 To jumlahTitik - 1 If TitikTerpilih(j) And daftarBiaya(u, j) <> Infinity Then . . .
2c6. Hitung jarak alternatif dari titik terpilih
jarakAlternatif = JarakKeTItikLain(u) + daftarBiaya(u, j)
2c7. Jika jarak yang melalui titik tujuan kurang dari nilai akumulasi jarak pada titik tersebut,
maka simpan data jarak yang baru
dan simpan indeks titik terpilih (titik u) sebagai data jalur sebelumnya dari titik tujuan
If jarakAlternatif < JarakKeTItikLain(j) Then JarakKeTItikLain(j) = jarakAlternatif JalurSebelumnya(j) = u End If
Hasil akhir adalah: (klik untuk perbesar gambar)
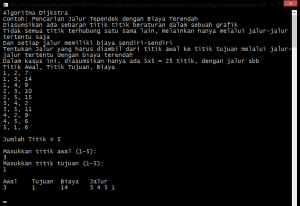
Jika diilustrasikan dalam gambar, maka model hasil akhirnya adalah sebagai berikut
Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:
[sdm_download id=”349″ fancy=”0″]
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.

Pada algoritma dijkstra disini kok tidak sama dengan yg lain?
Bukannya dijkstra ini hanya memilih node terpendek didepannya tanpa harus melihat hasil akhir jarak
Algoritma yang saya bahas pada website ini adalah berdasarkan dari referensi skrip yang saya pelajari, sehingga tidak menggunakan jurnal tertentu. Jika anda memiliki jurnal dengan contoh perhitungan yang tidak sama dengan pembahasan ini, maka sebaiknya silahkan gunakan jurnal tersebut sebagai panduan, dan tidak menggunakan skrip ini sebagai referensi.
gk sesuai dengan apa yang ada di codenya
tolong penjelasannya lebih sesuai dengan apa yang ada di code
orang yang awam akan bingung untuk memahaminya
Terima kasih atas umpan baliknya. Tetapi untuk saat ini cara penjelasan masih tidak akan mengalami perubahan. Silahkan mengambil contoh implementasi skrip untuk dapat melakukan pengujian secara langsung.