Regresi logistik / model logit, dalam statistika digunakan untuk prediksi probabilitas kejadian suatu peristiwa. Contoh yang dibahas kali ini adalah mengenai penentuan penerimaan pengajuan kredit sepeda motor baru berdasarkan kelompok data yang sudah ada
Ada banyak teknik optimasi yang dapat digunakan untuk proses pembelajaran. 2 teknik yang paling umum digunakan adalah teknik Newton-Raphson dan L-BFGS. Pada pembahasan ini, teknik yang digunakan adalah teknik Newton-Raphson.
Contoh variasi lain Regresi Logistik dapat dilihat dengan mengetikkan kata kunci “Regresi Logistik” pada website ini.
Diasumsikan ada 8 data pelanggan yang sudah diketahui datanya, yaitu Pelanggan A,B,C,D,E,F,G,H
Masing-masing pelanggan memiliki kriteria, yaitu umur, jenis kelamin, skor kepribadian, dan memiliki nilai hasil yaitu Diterima / Ditolak
Diasumsikan 8 data tersebut adalah sebagai berikut:
| Pelanggan | Umur | Jenis Kelamin | Skor Kepribadian | Hasil |
|---|---|---|---|---|
| Pelanggan A | 44 | Laki-laki | 3.55 | Diterima |
| Pelanggan B | 52 | Perempuan | 4.71 | Diterima |
| Pelanggan C | 60 | Perempuan | 6.56 | Ditolak |
| Pelanggan D | 56 | Laki-laki | 6.8 | Ditolak |
| Pelanggan E | 51 | Laki-laki | 6.94 | Ditolak |
| Pelanggan F | 46 | Perempuan | 6.52 | Ditolak |
| Pelanggan G | 48 | Laki-laki | 4.25 | Diterima |
| Pelanggan H | 58 | Perempuan | 5.71 | Diterima |
Contoh data awal adalah sebagai berikut:
Dim data(9)() As Double
data(0) = New Double() {44, -1, 3.55, 1}
data(1) = New Double() {52, +1, 4.71, 1}
data(2) = New Double() {60, +1, 6.56, 0}
data(3) = New Double() {56, -1, 6.8, 0}
data(4) = New Double() {51, -1, 6.94, 0}
data(5) = New Double() {46, +1, 6.52, 0}
data(6) = New Double() {48, -1, 4.25, 1}
data(7) = New Double() {58, +1, 5.71, 1}
Selanjutnya ada 2 orang pelanggan baru yang mengajukan kredit sepeda motor
Maka tentukan pelanggan ini nantinya akan termasuk dalam kelompok Diterima / Ditolak
Diasumsikan data awalnya adalah sebagai berikut:
| Pelanggan | Umur | Jenis Kelamin | Skor Kepribadian |
|---|---|---|---|
| Pelanggan I | 47 | Perempuan | 6.05 |
| Pelanggan J | 52 | Laki-Laki | 5 |
Contoh data baru adalah sebagai berikut:
data(8) = New Double() {47, +1, 6.05, -1}
data(9) = New Double() {52, -1, 5, -1}
* Tentukan jumlah iterasi yang digunakan dalam perhitungan koefisien Beta
Diasumsikan dalam kasus ini, jumlah iterasi adalah sebanyak 100 kali
Const jumlahIterasi As Integer = 100
* Tentukan epsilon
Perhitungan Koefisien Beta akan berhenti apabila nilai perbedaan antara nilai beta baru dan nilai beta sebelumnya kurang dari nilai epsilon
Artinya nilai koefisien beta sudah ditemukan
Diasumsikan dalam kasus ini, nilai epsilon adalah 0.01
Const epsilon As Double = 0.01
* Tentukan faktor lompatan
Perhitungan Koefisien Beta akan berhenti apabila nilai beta baru lebih dari sekian kali dari nilai beta sebelumnya
Artinya perhitungan algoritma sudah menyimpang dari jalurnya, sehingga nilai beta yang digunakan adalah nilai beta terbaik yang ditemukan sebelumnya
Diasumsikan dalam kasus ini, faktor lompatan adalah 1000
Const faktorLompatan As Double = 1000.0
Langkah-langkah penggunaan algoritma ini adalah
1. Hitung koefisien Beta untuk masing-masing kolom kriteria
Teknik yang digunakan dalam perhitungan ini adalah teknik Newton-Raphson
Penjelasan tentang fungsi tersebut akan dibahas pada perhitungan dibawah
Dim beta() As Double = hitungKoefisienBeta(contohDataKolomKriteria, contohDataKolomHasil, jumlahIterasi, epsilon, faktorLompatan)
2. Gunakan fungsi ini untuk menghitung nilai koefisien Beta untuk masing-masing kolom kriteria
teknik yang digunakan adalah teknik Newton-Raphson
Nilai pengembalian adalah koefisien beta b0 sebagai konstanta, b1 untuk kolom kriteria 1, dst sampai bn untuk kolom kriteria n
Private Function hitungKoefisienBeta(ByVal dataKolomKriteria()() As Double, ByVal dataKolomHasil() As Double, ByVal jumlahIterasi As Integer, ByVal epsilon As Double, ByVal faktorLompatan As Double) As Double()
- dataKolomKriteria adalah matriks data untuk kolom kriteria, kemudian nantinya ditambahkan kolom pertama yang semua berisi nilai 1.0 sebagai nilai dummy untuk konstanta b0
- dataKolomHasil adalah matriks data untuk kolom hasil, dengan nilai 0 atau 1
- jumlahIterasi adalah jumlah maksimal iterasi
- epsilon adalah salah satu variabel penghenti perhitungan,
perulangan akan berhenti apabila nilai yang baru berada diantara nilai epsilon dari nilai yang lama. Koefisien Beta telah ditemukan - faktorLompatan adalah salah satu variabel penghenti perhitungan,
perulangan akan berhenti apabila nilai yang baru adalah sekian kali dari nilai yang lama. Algorima sudah menyimpang dari jalur.
2a. Hitung nilai jawaban untuk semua data dengan nilai koefisien beta adalah 0
Dim probabilitas() As Double = hitungMatriksProb(dataKolomKriteria, matriksBeta)
* Gunakan fungsi ini untuk menghitung nilai jawaban untuk masing-masing data
Hitung nilai jawaban dengan rumus:
p = 1 / (1 + exp(-z) dimana z = b0x0 + b1x1 + b2x2 + b3x3 + . . .
jika matriks X berukuran 7 x 3 (kolom-kolom nya adalah: x0 = konstanta. 1.0, x1, x2)
maka matriks beta seharusnya berukuran 3 x 1
sehingga hasil dari matriks X dikali matriks beta adalah (7×3)(3×1) = (7×1)
Private Function hitungMatriksProb(ByVal dataKolomKriteria()() As Double, ByVal matriksBeta() As Double) As Double()
Dim barisMatriks As Integer = dataKolomKriteria.Length
Dim kolomMatriks As Integer = dataKolomKriteria(0).Length
If kolomMatriks <> matriksBeta.Length Then
Throw New Exception("Pada fungsi hitungMatriksProb, jumlah kolom matriks data tidak sama dengan jumlah baris matriks beta")
End If
Dim hasil(barisMatriks - 1) As Double
Dim z As Double = 0.0
Dim p As Double = 0.0
For i = 0 To barisMatriks - 1
z = 0.0
For j = 0 To kolomMatriks - 1
z += dataKolomKriteria(i)(j) * matriksBeta(j)
Next j
p = 1.0 / (1.0 + Math.Exp(-z))
hasil(i) = p
Next i
Return hasil
End Function
2b. Hitung tingkat kesalahan jawaban dengan menggunakan teknik MeanSquaredError
Dim mse As Double = MeanSquaredError(probabilitas, dataKolomHasil)
* Gunakan Fungsi ini untuk menghitung nilai MSE
Hitung tingkat kesalahan nilai jawaban menggunakan teknik Mean Squared Error
dihitung dengan rumus jumlah dari (kuadrat dari (nilai jawaban – nilai hasil pada matriks data)) / jumlah data
Nilai jawaban yang baru bisa jadi mengembalikan nilai MSE yang lebih tinggi, sehingga nilai jawaban ini tidak bisa dipakai
Private Function MeanSquaredError(ByVal probabilitas() As Double, ByVal dataKolomHasil() As Double) As Double
Dim barisProb As Integer = probabilitas.Length
If barisProb <> dataKolomHasil.Length Then
Throw New Exception("Pada fungsi MeanSquaredError, jumlah baris nilai jawaban tidak sama dengan jumlah baris matriks data")
End If
If barisProb = 0 Then
Return 0.0
End If
Dim hasil As Double = 0.0
For i = 0 To barisProb - 1
hasil += (probabilitas(i) - dataKolomHasil(i)) * (probabilitas(i) - dataKolomHasil(i))
Next i
Return hasil / barisProb
End Function
2c. Buat matriks beta baru untuk dibandingkan dengan nilai beta sebelumnya
Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah (poin 3)
Dim matriksBetaBaru() As Double = BuatMatriksBetaBaru(matriksBeta, dataKolomKriteria, dataKolomHasil, probabilitas) ' bisa mengembalikan nilai null
2d. Cek nilai beta baru apakah masih dalam rentang nilai epsilon.
Jika ya, maka hentikan perhitungan karena nilai beta sudah ditemukan
Dim bSt As Boolean = True For j = 0 To matriksBeta.Length - 1 If Math.Abs(matriksBeta(j) - matriksBetaBaru(j)) > epsilon Then bSt = False Exit For End If Next j If bSt Then Return matriksBetaTerbaik
2e. Cek nilai beta yang baru apakah sekian kali dari nilai beta yang lama.
Jika ya, maka hentikan perhitungan karena perhitungan telah menyimpang dari jalur
bSt = False For j = 0 To matriksBeta.Length - 1 If matriksBeta(j) = 0.0 Then bSt = False Exit For End If If Math.Abs(matriksBeta(j) - matriksBetaBaru(j)) / Math.Abs(matriksBeta(j)) > faktorLompatan Then bSt = True Exit For End If Next j If bSt Then Return matriksBetaTerbaik
2f. Hitung nilai jawaban untuk semua data dengan nilai koefisien beta yang baru
probabilitas = hitungMatriksProb(dataKolomKriteria, matriksBetaBaru)
2g. Hitung tingkat kesalahan jawaban baru dengan menggunakan teknik MeanSquaredError
Dim MSEbaru As Double = MeanSquaredError(probabilitas, dataKolomHasil)
2h. Bandingkan nilai MSE yang baru dan nilai MSE sebelumnya.
Jika nilai MSE jawaban yang baru ternyata lebih dari nilai MSE sebelumnya maka update nilai matriks beta menjadi rata-rata antara nilai beta baru dan nilai beta sebelumnya
Jika nilai MSE jawaban yang baru ternyata kurang dari nilai MSE sebelumnya maka ambil nilainya sebagai nilai matriks beta terbaik
If MSEbaru > mse Then MSEburukBerturutan += 1 If MSEburukBerturutan >= 4 Then Return matriksBetaTerbaik End If For j = 0 To matriksBetaBaru.Length - 1 matriksBeta(j) = matriksBetaBaru(j) Next j For k = 0 To matriksBeta.Length - 1 matriksBeta(k) = (matriksBeta(k) + matriksBetaBaru(k)) / 2.0 Next k mse = MSEbaru Else For j = 0 To matriksBetaBaru.Length - 1 matriksBeta(j) = matriksBetaBaru(j) Next j For j = 0 To matriksBeta.Length - 1 matriksBetaTerbaik(j) = matriksBeta(j) Next j mse = MSEbaru MSEburukBerturutan = 0 End If
2i. Lakukan perulangan point 2c – 2h sebanyak jumlah iterasi, kecuali perulangan telah dihentikan karena memenuhi kondisi penghentian perulangan
3. Gunakan fungsi ini untuk membuat nilai beta yang baru
Fungsi ini mengandung inti perhitungan dengan teknik Newton-Raphson
nilai beta yang baru dihitung dengan rumus:
bt = bt-1 + inv(X’Wt-1X)X'(y – pt-1)
dimana:
bt adalah nilai beta yang baru
bt-1 adalah nilai beta yang sebelumnya
X’ adalah transpos matriks dari matriks X
Wt-1 adalah nilai bobot matriks sebelumnya
y adalah nilai matriks untuk Kolom Hasil
pt-1 adalah nilai probabilitas yang lama, dihitung dengan rumus 1.0 / (1.0 + exp(-z) dimana z = b0x0 + b1x1 + . . .)
Private Function BuatMatriksBetaBaru(ByVal matriksBetaLama() As Double, ByVal dataKolomKriteria()() As Double, ByVal dataKolomHasil() As Double, ByVal probabilitasLama() As Double) As Double() Dim XTranspos()() As Double = HitungTransposMatriks(dataKolomKriteria) ' X' Dim XTilda()() As Double = HitungTildaMatriks(probabilitasLama, dataKolomKriteria) ' WX atau X~ Dim XTransposXTilda()() As Double = HitungPerkalianMatriks(XTranspos, XTilda) ' X'WX Dim InverseXTransposXTilda()() As Double = HitungInversMatriks(XTransposXTilda) ' Invers(X'WX) If InverseXTransposXTilda Is Nothing Then Return Nothing Dim InverseXTransposXTildaXTranspos()() As Double = HitungPerkalianMatriks(InverseXTransposXTilda, XTranspos) ' Invers(X'WX)X' Dim YP() As Double = hitungPenguranganMatriks(dataKolomHasil, probabilitasLama) ' y-p Dim InverseXTransposXTildaXTransposYP() As Double = hitungPerkalianMatriksYP(InverseXTransposXTildaXTranspos, YP) ' Invers(X'WX)X'(y-p) Dim hasil() As Double = hitungPenjumlahanMatriks(matriksBetaLama, InverseXTransposXTildaXTransposYP) ' beta + Invers(X'WX)X'(y-p) Return hasil End Function
3a. Gunakan fungsi ini untuk menghitung transpos matriks
Private Function HitungTransposMatriks(ByVal matriks()() As Double) As Double()()
Dim rows As Integer = matriks.Length
Dim cols As Integer = matriks(0).Length
Dim hasil(cols - 1)() As Double
For i = 0 To cols - 1
hasil(i) = New Double(rows - 1) {}
Next i
For i = 0 To rows - 1
For j = 0 To cols - 1
hasil(j)(i) = matriks(i)(j)
Next j
Next i
Return hasil
End Function
3b. Gunakan fungsi ini untuk menghitung matriks tilda (~)
Private Function HitungTildaMatriks(ByVal probabilitas() As Double, ByVal dataKolomKriteria()() As Double) As Double()()
' matriks Wt-1 berukuran nxn sehingga ukurannya bisa sangat besar
' Karena matriks W diperoleh dari matriks probabilitas, maka matriks W hanya berisikan nilai pada bagian diagonal saja
' sehingga daripada menghitung perkalian matriks W dengan ukuran nxn, cukup menggunakan matriks probabilitas dengan ukuran n, dan tidak perlu menghitung matriks W
Dim barisProb As Integer = probabilitas.Length
Dim barisMatriks As Integer = dataKolomKriteria.Length
Dim kolomMatriks As Integer = dataKolomKriteria(0).Length
If barisProb <> barisMatriks Then
Throw New Exception("Pada fungsi hitungTildaMatriks, Jumlah baris nilai jawaban tidak sama dengan jumlah baris matriks data")
End If
Dim hasil(barisProb - 1)() As Double
For i = 0 To barisProb - 1
hasil(i) = New Double(kolomMatriks - 1) {}
Next i
For i = 0 To barisProb - 1
For j = 0 To kolomMatriks - 1
hasil(i)(j) = probabilitas(i) * (1.0 - probabilitas(i)) * dataKolomKriteria(i)(j) ' p(1-p)
Next j
Next i ' i
Return hasil
End Function
3c. Gunakan fungsi ini untuk menghitung penjumlahan matriks
Private Function hitungPenjumlahanMatriks(ByVal matriksA() As Double, ByVal matriksB() As Double) As Double()
If matriksA.Length <> matriksB.Length Then
Throw New Exception("Pada fungsi hitungPenjumlahanMatriks, Ukuran matriks A dan B tidak sama")
End If
Dim hasil(matriksA.Length - 1) As Double
For i = 0 To matriksA.Length - 1
hasil(i) = matriksA(i) + matriksB(i)
Next i
Return hasil
End Function
3d. Gunakan fungsi ini untuk menghitung pengurangan matriks
Private Function hitungPenguranganMatriks(ByVal matriksA() As Double, ByVal matriksB() As Double) As Double()
If matriksA.Length <> matriksB.Length Then
Throw New Exception("Pada fungsi hitungPenguranganMatriks, Ukuran matriks A dan B tidak sama")
End If
Dim hasil(matriksA.Length - 1) As Double
For i = 0 To matriksA.Length - 1
hasil(i) = matriksA(i) - matriksB(i)
Next i
Return hasil
End Function
3e. Gunakan fungsi ini untuk menghitung perkalian 2 matriks dengan ukuran sama
Private Function HitungPerkalianMatriks(ByVal matriksA()() As Double, ByVal matriksB()() As Double) As Double()()
Dim matriksARows As Integer = matriksA.Length
Dim matriksACols As Integer = matriksA(0).Length
Dim matriksBRows As Integer = matriksB.Length
Dim matriksBCols As Integer = matriksB(0).Length
If matriksACols <> matriksBRows Then
Throw New Exception("Pada fungsi hitungPerkalianMatriks, Ukuran Matriks A dan B tidak sama")
End If
Dim hasil(matriksARows - 1)() As Double
For i = 0 To matriksARows - 1
hasil(i) = New Double(matriksBCols - 1) {}
Next i
For i = 0 To matriksARows - 1
For j = 0 To matriksBCols - 1
For k = 0 To matriksACols - 1
hasil(i)(j) += matriksA(i)(k) * matriksB(k)(j)
Next k
Next j
Next i
Return hasil
End Function
3f. Gunakan fungsi ini untuk menghitung perkalian matriks dengan ukuran tidak sama
Private Function hitungPerkalianMatriksYP(ByVal matriks()() As Double, ByVal YP() As Double) As Double()
If matriks(0).Length <> YP.Length Then
Throw New Exception("Pada fungsi hitungPerkalianMatriksYP, Jumlah kolom Matriks A tidak sama dengan jumlah baris matirks B")
End If
Dim hasil(matriks.Length - 1) As Double
For i = 0 To matriks.Length - 1
For j = 0 To matriks(0).Length - 1
hasil(i) += matriks(i)(j) * YP(j)
Next j
Next i
Return hasil
End Function
3g. Gunakan fungsi ini untuk menghitung invers matriks
Private Function HitungInversMatriks(ByVal matriks()() As Double) As Double()()
Dim n As Integer = matriks.Length
'Salin Matriks
Dim hasil(n - 1)() As Double
For i = 0 To n - 1
hasil(i) = New Double(matriks(0).Length - 1) {}
For j = 0 To matriks(0).Length - 1
hasil(i)(j) = matriks(i)(j)
Next j
Next i
Dim permutasi() As Integer
Dim matriksLU()() As Double = DekomposisiMatriks(matriks, permutasi)
If matriksLU Is Nothing Then
Return Nothing
End If
Dim b(n - 1) As Double
For i = 0 To n - 1
For j = 0 To n - 1
If i = permutasi(j) Then
b(j) = 1.0
Else
b(j) = 0.0
End If
Next j
Dim x() As Double = hitungPersamaanAxB(matriksLU, b)
For j = 0 To n - 1
hasil(j)(i) = x(j)
Next j
Next i
Return hasil
End Function
3h. Gunakan fungsi ini untuk menghitung dekomposisi matriks
Metode yang digunakan untuk mendekomposisi matriks adalah metode Dolittle
Private Function DekomposisiMatriks(ByVal matriks()() As Double, ByRef permutasi() As Integer) As Double()()
If matriks.Length <> matriks(0).Length Then
Throw New Exception("Pada fungsi dekomposisiMatriks, ukuran baris dan kolom Matriks harus sama.")
End If
Dim n As Integer = matriks.Length
'Salin Matriks
Dim hasil(n - 1)() As Double
For i = 0 To n - 1
hasil(i) = New Double(matriks(0).Length - 1) {}
For j = 0 To matriks(0).Length - 1
hasil(i)(j) = matriks(i)(j)
Next j
Next i
permutasi = New Integer(n - 1) {}
For i = 0 To n - 1
permutasi(i) = i
Next i
Dim ajj, aij As Double
For j = 0 To n - 2
Dim nilaiMaksimalBaris As Double = Math.Abs(hasil(j)(j)) ' nilai terbesar pada baris tersebut
'Cari pivot
Dim barisPivot As Integer = j
For i = j + 1 To n - 1
aij = Math.Abs(hasil(i)(j))
If aij > nilaiMaksimalBaris Then
nilaiMaksimalBaris = aij
barisPivot = i
End If
Next i
' Jika nilai terbesar tidak berada di pivot, tukar baris tersebut dengan baris sekarang
' dan tukar baris yang sama pada matriks permutasi
If barisPivot <> j Then
Dim rowPtr() As Double = hasil(barisPivot)
hasil(barisPivot) = hasil(j)
hasil(j) = rowPtr
Dim tmp As Integer = permutasi(barisPivot)
permutasi(barisPivot) = permutasi(j)
permutasi(j) = tmp
End If
' Jika setelah penukaran baris, ternyata nilai diagonal adalah 0, maka hentikan perhitungan
ajj = hasil(j)(j)
If Math.Abs(ajj) < 0.00000001 Then
Return Nothing
End If
'Lakukan dekomposisi matriks untuk mendapatkan matriks LU
For i = j + 1 To n - 1
aij = hasil(i)(j) / ajj
hasil(i)(j) = aij
For k = j + 1 To n - 1
hasil(i)(k) -= aij * hasil(j)(k)
Next k
Next i
Next j
Return hasil
End Function
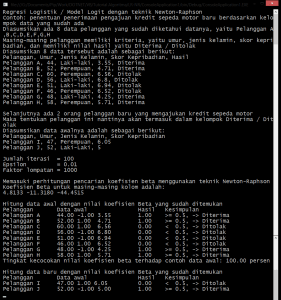
4. Setelah memperoleh nilai koefisien beta, cari nilai jawaban untuk masing-masing contoh data
Dim probabilitas() As Double = hitungMatriksProb(contohDataKolomKriteria, beta)
5. Jika nilai probabilitas lebih dari 0.5, maka data baru tersebut termasuk dalam nilai hasil Diterima
Jika nilai probabilitas kurang dari 0.5, maka data baru tersebut termasuk dalam nilai hasil Ditolak
If probabilitas(i) >= 0.5 Then
Console.WriteLine(">= 0.5, -> Diterima")
If data(i)(3) >= 0.5 Then
jumlahBenar += 1
Else
jumlahSalah += 1
End If
ElseIf probabilitas(i) < 0.5 Then
Console.WriteLine("< 0.5, -> Ditolak")
If data(i)(3) < 0.5 Then
jumlahBenar += 1
Else
jumlahSalah += 1
End If
End If
6. Lakukan poin 4 dan 5 untuk semua data baru
Hasil akhir adalah: (klik untuk perbesar gambar)
Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:
[sdm_download id=”589″ fancy=”0″]
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.
