Algoritma B&B (Branch and Bound) adalah salah satu algoritma yang digunakan untuk pencarian jalur. Contoh yang dibahas kali ini adalah mengenai pencarian jalur yang melalui semua titik dengan biaya terendah.
Algoritma ini memiliki 2 prinsip, yaitu:
- Algoritma ini akan melakukan perhitungan secara rekursif, akan memecah masalah kedalam masalah-masalah kecil, sambil tetap menghitung nilai terendah / terbaik. Proses ini dinamakan branching
- Jika branching diterapkan secara sendirian, maka hasilnya akan tetap mencari setiap kemungkinan yang ada. Untuk meningkatkan performa, algoritma ini akan melakukan pencatatan biaya minimum sebagai bound dalam setiap perhitungan, sehingga untuk calon hasil jawaban yang diperkirakan akan melebihi bound akan dibuang karena tidak mungkin akan mencapai nilai terbaik
Diasumsikan ada 5 titik yang harus dilalui semuanya, yaitu A,B,C,D,E
semua titik tidak terhubung secara langsung dengan titik-titik lainnya, melainkan hanya melalui jalur tertentu saja
setiap jalur juga memiliki biaya sendiri-sendiri
maka tentukan jalur yang harus diambil untuk mengelilingi semua titik yang ada
Diasumsikan data jalur yang tersedia adalah sebagai berikut
| Titik awal | Titik Tujuan | Biaya |
|---|---|---|
| Titik A | Titik B | 10 |
| Titik A | Titik E | 11 |
| Titik B | Titik A | 12 |
| Titik B | Titik C | 20 |
| Titik B | Titik D | 6 |
| Titik B | Titik E | 9 |
| Titik C | Titik B | 15 |
| Titik C | Titik D | 14 |
| Titik D | Titik B | 7 |
| Titik D | Titik C | 5 |
| Titik E | Titik C | 8 |
| Titik E | Titik D | 13 |
Jika diilustrasikan dalam gambar, maka model data awal adalah sebagai berikut
Sebelum masuk kedalam langkah-langkah pembahasan algoritma, ada beberapa konstanta atau parameter yang harus diketahui, yaitu:
* Tentukan jumlah titik yang harus dihubungkan
Diasumsikan dalam kasus ini, jumlah titik ada 5 buah
Const jumlahTitik As Integer = 5
Langkah-langkah penggunaan algoritma ini adalah
1. Lakukan inisialisasi daftar jalur sesuai dengan data yang tersedia
Terdapat matriks berukuran [jumlah titik x jumlah titik] untuk menyimpan jalur dari masing-masing titik
Jika tidak ada jalur diantara 2 titik, maka nilai jalurnya adalah 0
Dim daftarBiaya(,) As Double = New Double(jumlahTitik - 1, jumlahTitik - 1) { _
{0, 10, 0, 0, 11}, _
{12, 0, 20, 6, 9}, _
{0, 15, 0, 14, 0}, _
{0, 7, 5, 0, 0}, _
{0, 0, 8, 13, 0} _
}
2. Hitung rata-rata biaya pada semua data
Nilai ini nantinya akan digunakan untuk perkiraan nilai biaya apakah akan melebihi bound atau tidak
Dim rata2 As Integer = 0 Dim count As Integer = 0 For i As Integer = 0 To jumlahTitik - 1 For j As Integer = 0 To jumlahTitik - 1 If daftarBiaya(i, j) <> 0 Then rata2 += daftarBiaya(i, j) count += 1 End If Next Next rata2 /= count
3. Lakukan perhitungan pencarian jalur melalui semua titik yang ada
Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah ini (poin 3a)
CariJalurTerbaik(jumlahTitik, rata2, daftarBiaya, jalurTerbaik, BiayaTerbaik)
Memasuki perhitungan pada fungsi CariJalurTerbaik
3a. Lakukan perhitungan pada masing-masing titik (poin 3a1 – 3a3)
For i As Integer = 0 To jumlahTitik - 1 . . .
3a1. Beri nilai awal calon jalur dengan nilai -1
For j As Integer = 0 To jumlahTitik - 1 calonJalur(j) = -1 Next
3a2. Lakukan perhitungan pada masing-masing titik selain titik awal (poin 3a2a – 3a2c)
For j As Integer = 0 To jumlahTitik - 1 If daftarBiaya(i, j) <> 0 Then . . .
3a2a. Masukkan titik awal pada calon jalur yang sedang dihitung
calonJalur(0) = i
3a2b. Inisialisasi titik titik yang sudah dihitung dengan nilai false,
kemudian tandai titik awal dengan nilai True agar tidak dapat digunakan dalam perhitungan selanjutnya
Dim titikTerpilih(jumlahTitik - 1) As Boolean titikTerpilih(i) = True
3a2c. Lakukan pencarian jalur dimulai dari titik awal yang terpilih
Penjelasan lebih detail tentang fungsi ini dapat dilihat pada penjelasan dibawah ini
CariJalur(jumlahTitik, rata2, daftarBiaya, jalur, biaya, titikTerpilih, calonJalur, totalCalonJalur, 1)
Memasuki Perhitungan pada fungsi CariJalur
3a2c1. Jika semua titik sudah terpilih, maka bandingkan total biaya jalur ini dengan total biaya terbaik
Jika total biaya jalur ini kurang dari total biaya terbaik, maka ambil total jalur ini sebagai jalur terbaik
If jumlahTitikTerpilih >= jumlahTitik Then If totalCalonJalur < biayaTerbaik Then biayaTerbaik = totalCalonJalur Array.Copy(calonJalur, jalurTerbaik, jumlahTitik) End If . . .
3a2c2. Lakukan perhitungan dibawah ini apabila kondisi diatas tidak terpenuhi (poin 3a2c2a – 3a2c2c)
Else . . .
3a2c2a. Lakukan pengecekan terhadap sisa titik yang akan dihitung
Apabila perkiraan sisa titik akan melebihi bound biaya terbaik, maka hentikan perhitungan
Dim sisaTitik As Integer = jumlahTitik - jumlahTitikTerpilih If totalCalonJalur + rata2 * sisaTitik >= biayaTerbaik Then Return End If
3a2c2b. Dapatkan indeks titik yang terakhir kali dihitung untuk digunakan sebagai titik awal pada perhitungan berikutnya
Dim idxTitikTerakhir As Integer = calonJalur(jumlahTitikTerpilih - 1)
3a2c2c. Lakukan perhitungan pada masing-masing titik untuk titik-titik yang belum terpilih dan memiliki jarak dengan titik terakhir (poin 3a2c2c1 – 3a2c2c3)
For i As Integer = 0 To jumlahTitik - 1 If titikTerpilih(i) = False AndAlso daftarBiaya(idxTitikTerakhir, i) <> 0 Then . . .
3a2c2c1. Masukkan titik ini sebagai titik berikutnya pada calon jalur yang sedang dihitung
dan tandai titik ini sebagai titik yang sudah terpilih
calonJalur(jumlahTitikTerpilih) = i titikTerpilih(i) = True
3a2c2c2. Lakukan proses percabangan / branch,
yaitu Ulangi fungsi ini menggunakan titik yang baru sebagai titik awal
CariJalur(jumlahTitik, rata2, daftarBiaya, jalurTerbaik, biayaTerbaik, titikTerpilih, _ calonJalur, totalCalonJalur + daftarBiaya(idxTitikTerakhir, i), jumlahTitikTerpilih + 1)
3a2c2c3. Setelah semua kemungkinan cabang pada titik tersebut sudah dihitung,
maka keluarkan titik ini dari calon jalur yang sedang dihitung
dan tandai titik ini sebagai titik yang belum terpilih
calonJalur(jumlahTitikTerpilih) = -1 titikTerpilih(i) = False
3a3. Jika biaya jalur yang baru ditemukan lebih baik dari biaya jalur terbaik,
maka ambil jalur tersebut sebagai jalur terbaik
If biaya < biayaTerbaik Then biayaTerbaik = biaya Array.Copy(jalur, jalurTerbaik, jumlahTitik) End If
Hasil akhir adalah: (klik untuk perbesar gambar)
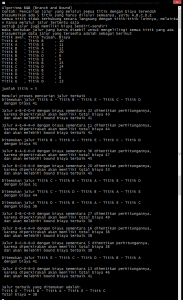
Jika diilustrasikan dalam gambar, maka model hasil akhirnya adalah sebagai berikut
Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:
[sdm_download id=”1712″ fancy=”0″]
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.

mohon izin bertanya, apa perbedaan antara algoritma branch and bound dengan algoritma ant colony? apakah terkait dengan batasan yg dimiliki?
Menurut saya algoritma ACO adalah algoritma untuk menyelesaikan permasalahan optimasi. Walaupun implementasi algoritma lebih sulit, tetapi penggunaan algoritma dapat diterapkan pada permasalahan yang bukan pencarian jalur. Sedangkan algoritma Branch and Bound memiliki implementasi yang lebih rendah tingkat kesulitannya tetapi tidak dapat menyelesaikan permasalahan optimasi.
mau tanya itu source code nya di vb ya? tapi kok outputnya cmd?
Ya, betul. Modul ini saya rancang dalam bahasa visual basic .NET dalam tipe konsol. Untuk menjalankan modul ini, silahkan membuat proyek baru dengan tipe “Console Application”, kemudian salin isi skrip pada file yang disediakan atau anda bisa menimpa langsung modul kosong pada proyek tersebut.