Algoritma Johnson adalah salah satu algoritma yang digunakan untuk pencarian jalur. Contoh yang dibahas kali ini adalah mengenai pencarian jalur yang melalui semua titik dengan jarak terpendek.
Secara singkat, Algoritma ini adalah penggabungan dari Algoritma Bellman-Ford dan Algoritma Dijkstra yang sudah dijelaskan sebelumnya. Setelah mendapatkan nilai jarak yang baru dengan menggunakan Bellman-Ford, maka lakukan proses pembobotan ulang untuk menghilangkan nilai jarak negatif. Jika semua jarak sudah bernilai positif, maka pencarian jalur dapat dilakukan dengan metode Dijkstra. Setelah jalur ditemukan, kembalikan nilai bobot seperti semula untuk mencatat total bobot yang sebenarnya
Diasumsikan ada sebaran titik yang harus dilalui semuanya
semua titik tidak terhubung secara langsung dengan titik-titik lainnya, melainkan hanya melalui jalur tertentu saja
setiap jalur juga memiliki bobot sendiri-sendiri
Tentukan Jalur yang harus diambil untuk mengelilingi semua titik dengan jarak terpendek
Diasumsikan data jalur yang tersedia adalah sebagai berikut
| Titik awal | Titik Tujuan | Jarak |
|---|---|---|
| Titik A | Titik B | 6 |
| Titik A | Titik E | 7 |
| Titik B | Titik C | 5 |
| Titik B | Titik D | -4 |
| Titik B | Titik E | 8 |
| Titik C | Titik B | -2 |
| Titik D | Titik C | 7 |
| Titik E | Titik C | -3 |
| Titik E | Titik D | 9 |
Contoh data awal adalah sebagai berikut:
bobotA.Add(6) bobotA.Add(7) garisA.Add(titikB) garisA.Add(titikE) bobotB.Add(5) bobotB.Add(-4) bobotB.Add(8) garisB.Add(titikC) garisB.Add(titikD) garisB.Add(titikE) bobotC.Add(-2) garisC.Add(titikB) bobotD.Add(7) garisD.Add(titikC) bobotE.Add(-3) bobotE.Add(9) garisE.Add(titikC) garisE.Add(titikD) titikA.tetangga = garisA titikA.bobot = bobotA titikB.tetangga = garisB titikB.bobot = bobotB titikC.tetangga = garisC titikC.bobot = bobotC titikD.tetangga = garisD titikD.bobot = bobotD titikE.tetangga = garisE titikE.bobot = bobotE Dim daftarTitik As New List(Of Titik)() daftarTitik.Add(titikA) daftarTitik.Add(titikB) daftarTitik.Add(titikC) daftarTitik.Add(titikD) daftarTitik.Add(titikE)
Jika diilustrasikan dalam gambar, maka model data awal adalah sebagai berikut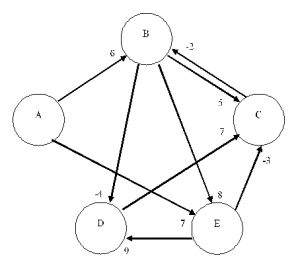
Langkah-langkah penggunaan algoritma ini adalah
1. Lakukan proses pencarian jalur dengan metode Bellman-Ford
Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah ini (poin 1a – 1e)
If BellmanFord(titikTujuan, daftarTitik) Then . . .
Memasuki perhitungan pada fungsi BellmanFord
1a. Lakukan inisialisasi variabel titik tujuan sebanyak jumlah titik
variabel ini digunakan untuk menyimpan titik tujuan pada masing-masing indeks titik
Beri nilai awal pada pasing-masing titik tujuan dengan angka -1
titikTujuan = New Integer(daftarTitik.Count - 1) {}
For i As Integer = 0 To titikTujuan.Length - 1
titikTujuan(i) = -1
Next
1b. Beri nilai awal jarak pada titik awal dengan 0
daftarTitik(0).jarak = 0
1c. Lakukan perulangan pada semua titik awal secara terurut
Untuk masing-masing titik awal, lakukan perulangan pada semua titik tujuan yang ditemukan (poin 1c1 – 1c2)
For i As Integer = 0 To daftarTitik.Count - 2 Dim titikAwalTerpilih As Titik = daftarTitik(i) For j As Integer = 0 To titikAwalTerpilih.tetangga.Count - 1 Dim titikTujuanTerpilih As Titik = titikAwalTerpilih.tetangga(j) . . .
1c1. jika jarak dari titik tujuan lebih dari jarak titik awal ditambah bobotnya,
maka pilih titik awal ini sebagai titik tujuan
If titikTujuanTerpilih.jarak > titikAwalTerpilih.jarak + bobot Then titikTujuanTerpilih.jarak = titikAwalTerpilih.jarak + bobot titikTujuan(titikTujuanTerpilih.Id) = titikAwalTerpilih.Id End If
1c2. lakukan perulangan terhadap semua titik tetangga dari titik tujuan (poin 1c2a)
For k As Integer = 0 To titikTujuanTerpilih.tetangga.Count - 1 Dim titikTujuanTetanggaTerpilih As Titik = titikTujuanTerpilih.tetangga(k) . . .
1c2a. jika jarak dari titik tetangga lebih dari jarak titik tujuan ditambah bobotnya,
maka pilih titik tetangga ini sebagai titik tujuan
If titikTujuanTetanggaTerpilih.jarak > titikTujuanTerpilih.jarak + bobot Then titikTujuanTetanggaTerpilih.jarak = titikTujuanTerpilih.jarak + bobot titikTujuan(titikTujuanTetanggaTerpilih.Id) = titikTujuanTerpilih.Id End If
1d. Lakukan perulangan pada semua titik awal dan titik tujuan
jika jarak dari titik tujuan lebih dari jarak titik awal ditambah bobotnya,
maka hentikan perhitungan dan kembalikan nilai fungsi ini dengan nilai false
For i As Integer = 0 To daftarTitik.Count - 1 Dim titikAwalTerpilih As Titik = daftarTitik(i) For j As Integer = 0 To titikAwalTerpilih.tetangga.Count - 1 Dim titikTujuanTerpilih As Titik = titikAwalTerpilih.tetangga(j) Dim bobot As Integer = titikAwalTerpilih.bobot(j) If titikTujuanTerpilih.jarak > titikAwalTerpilih.jarak + bobot Then Return False End If Next Next
1e. Jika kondisi nomor 4 tidak terpenuhi, maka kembalikan nilai fungsi ini dengan nilai true
Return True
2. Catat hasil sementara untuk masing-masing jawaban jarak yang ditemukan
Kemudian hitung total jarak dengan menjumlahkan semua jarak yang ditemukan
For i As Integer = 0 To titikTujuan.Count - 1
If titikTujuan(i) <> -1 Then
For iCount As Integer = 0 To daftarTitik(titikTujuan(i)).tetangga.Count - 1
If i = daftarTitik(titikTujuan(i)).tetangga(iCount).Id Then
jarak = daftarTitik(titikTujuan(i)).tetangga(iCount).jarak
totalJarak += jarak
Exit For
End If
Next
Console.WriteLine("Jalur " & i & " adalah dari titik " & daftarTitik(titikTujuan(i)).nama & " ke titik " & daftarTitik(i).nama & " dengan jarak " & jarak)
End If
Next
3. Lakukan pembobotan ulang pada masing-masing bobot yang ada untuk menghilangkan bobot dengan nilai negatif
Nilai bobot yang baru dihitung dengan rumus
garis[u][v] = garis[u][v] + jarak[u] – jarak[v]
For i As Integer = 0 To daftarTitik.Count - 1
Dim titikAwalTerpilih As Titik = daftarTitik(i)
For j As Integer = 0 To titikAwalTerpilih.tetangga.Count - 1
Dim titikTujuanTerpilih As Titik = titikAwalTerpilih.tetangga(j)
titikAwalTerpilih.bobot(j) += titikAwalTerpilih.jarak - titikTujuanTerpilih.jarak
Console.WriteLine("Titik " & titikAwalTerpilih.nama & " , Titik " & titikTujuanTerpilih.nama & " , " & titikAwalTerpilih.bobot(j))
Next
Next
4. Setelah tidak ada bobot dengan nilai negatif,
maka lakukan pencarian jalur terpendek dari masing-masing titik menggunakan metode Dijkstra
Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah ini (poin 4a – 4d)
For i As Integer = 0 To daftarTitik.Count - 1 Dim minBobot As Double = Double.MaxValue Dim JumlahTitikDilewati As Integer = 0 Dim jalur As String = Dijkstra(daftarTitik.Count, i, daftarTitik, minBobot, JumlahTitikDilewati) . . .
Memasuki perhitungan pada fungsi Dijkstra
4a. Inisialisasi Array Jarak ke titik lain
Pada array tersebut, selain indeks titik awal, beri nilai jarak dengan angka yang sangat besar
Dim JarakKeTItikLain(jumlahTitik - 1) As Double For j As Integer = 0 To jumlahTitik - 1 JarakKeTItikLain(j) = Double.MaxValue Next j JarakKeTItikLain(idxTitikAwal) = 0
4b. Inisialisasi Array Titik Terpilih menjadi benar semua, artinya semua titik tersedia untuk dihitung
Kemudian beri nilai array Jalur Sebelumnya menjadi -1
Dim JalurSebelumnya(jumlahTitik - 1) As Integer Dim TitikTerpilih(jumlahTitik - 1) As Boolean For j As Integer = 0 To jumlahTitik - 1 TitikTerpilih(j) = True JalurSebelumnya(j) = -1 Next j
4c. Lakukan perhitungan selama masih ada titik yang belum dihitung (poin 4c1 – 4c7)
4c1. Beri nilai awal jarak dengan nilai yang sangat besar
jarak = Double.MaxValue
4c2. Untuk masing-masing titik yang sudah terpilih,
Hitung jarak terpendek ke titik lain, dan simpan indeks titik dengan jarak terpendek
For i As Integer = 0 To jumlahTitik - 1 If TitikTerpilih(i) Then If JarakKeTItikLain(i) < jarak Then jarak = JarakKeTItikLain(i) u = i End If End If Next i
4c3. Jika nilai jarak tidak ditemukan, maka perhitungan selesai karena tidak ada titik lain yang menghasilkan jarak lebih pendek
If jarak = Double.MaxValue Then Exit Do
4c4. Beri nilai false untuk titik terpilih agar tidak dihitung pada perulangan berikutnya
TitikTerpilih(u) = False
4c5. Cari semua titik tujuan dari indeks titik yang terpilih (indeks u)
Lakukan perhitungan berikutnya apabila titik tujuan tersebut sudah terpilih dan terdapat jarak yang sah antara titik u dan titik tujuan
For j As Integer = 0 To jumlahTitik - 1 If TitikTerpilih(j) Then Dim titikAwal As Titik = daftarTitik(u) For k As Integer = 0 To titikAwal.tetangga.Count - 1 If j = titikAwal.tetangga(k).Id Then . . .
4c6. Hitung jarak alternatif dari titik terpilih
jarakAlternatif = JarakKeTItikLain(u) + titikAwal.bobot(k)
4c7. Jika jarak yang melalui titik tujuan kurang dari nilai akumulasi jarak pada titik tersebut,
maka simpan data jarak yang baru
dan simpan indeks titik terpilih (titik u) sebagai data jalur sebelumnya dari titik tujuan
If jarakAlternatif < JarakKeTItikLain(j) Then JarakKeTItikLain(j) = jarakAlternatif JalurSebelumnya(j) = u End If
4d. Setelah perhitungan pada poin diatas selesai,
maka untuk masing-masing titik,
lakukan pencatan jalur dimulai dari titik tersebut dan hitung jumlah titik yang dilewati jalur tersebut
Ambil jalur dengan jumlah titik paling banyak dan bobot yang paling rendah
For i As Integer = 0 To daftarTitik.Count - 1 Dim jumlahTitikPadaJalur As Integer = 1 Dim s As String = CariJalur(idxTitikAwal, i, JalurSebelumnya, jumlahTitikPadaJalur) If maksJumlahTitikDilewati < jumlahTitikPadaJalur Or _ (maksJumlahTitikDilewati = jumlahTitikPadaJalur And minBobot < JarakKeTItikLain(i)) Then maksJumlahTitikDilewati = jumlahTitikPadaJalur minBobot = JarakKeTItikLain(i) jalur = s JumlahTitikDilewati = jumlahTitikPadaJalur End If Next
5. Setelah menemukan jalur terbaik, maka kembalikan nilai bobot seperti semua
Untuk mengembalikan nilai bobot seperti semula dapat menggunakan rumus
garis[u][v] = garis[u][v] + jarak[v] – jarak[u]
For i As Integer = 0 To daftarTitik.Count - 1
Dim titikAwalTerpilih As Titik = daftarTitik(i)
For j As Integer = 0 To titikAwalTerpilih.tetangga.Count - 1
Dim titikTujuanTerpilih As Titik = titikAwalTerpilih.tetangga(j)
titikAwalTerpilih.bobot(j) += titikTujuanTerpilih.jarak - titikAwalTerpilih.jarak
Console.WriteLine("Titik " & titikAwalTerpilih.nama & " , Titik " & titikTujuanTerpilih.nama & " , " & titikAwalTerpilih.bobot(j))
Next
Next
6. Hitung total bobot dengan menjumlahkan semua bobot pada jalur yang ditemukan
For i As Integer = 0 To titik.Length - 3
Dim tAwal As Titik = daftarTitik(titik(i))
Dim tTujuan As Titik = daftarTitik(titik(i + 1))
For j As Integer = 0 To tAwal.tetangga.Count - 1
If tAwal.tetangga(j).Id = tTujuan.Id Then
bobot = tAwal.bobot(j)
totalBobot += bobot
Exit For
End If
Next
Console.WriteLine("Jalur " & i + 1 & " adalah dari titik " & tAwal.nama & " ke titik " & tTujuan.nama & " dengan bobot " & bobot)
Next
* Agar dapat menjalankan skrip diatas, maka diperlukan sebuah Class Titik untuk menampung semua data titik beserta jalurnya. Deklarasi Class Titik adalah sebagai berikut:
Class Titik
Private m_jarak As Integer
Private m_id As Integer
Private m_nama As String
Private m_bobot As List(Of Integer)
Private m_tetangga As List(Of Titik)
Public Sub New(jarak As Integer, id As Integer, nama As String)
Me.m_jarak = jarak
Me.m_id = id
Me.m_nama = nama
m_bobot = New List(Of Integer)()
m_tetangga = New List(Of Titik)()
End Sub
Public Property jarak() As Integer
Get
Return m_jarak
End Get
Set(value As Integer)
m_jarak = value
End Set
End Property
Public Property Id() As Integer
Get
Return m_id
End Get
Set(value As Integer)
m_id = value
End Set
End Property
Public Property nama() As String
Get
Return m_nama
End Get
Set(value As String)
m_nama = value
End Set
End Property
Public Property tetangga() As List(Of Titik)
Get
Return m_tetangga
End Get
Set(value As List(Of Titik))
m_tetangga = value
End Set
End Property
Public Property bobot() As List(Of Integer)
Get
Return m_bobot
End Get
Set(value As List(Of Integer))
m_bobot = value
End Set
End Property
End Class
Hasil akhir adalah: (klik untuk perbesar gambar)
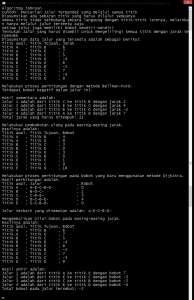
Jika diilustrasikan dalam gambar, maka model hasil akhirnya adalah sebagai berikut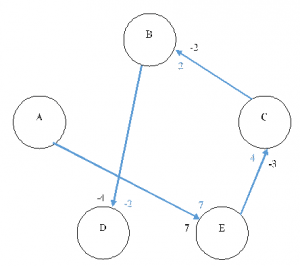
Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.

Saya tertarik mempelajari algoritma johnson ini min, setelah saya baca ada pertanyaan ni min
Dari penjelasan diatas kan algoritma johnson menggabungkan bellman-ford dan dijkstra, dimana bellman-ford digunakan untuk menghilangkan nilai negatif pada jarak antar titik dan dijkstra untuk mencari jalur terpendeknya
Nah bagaimana jika dalam contoh kasusnya tidak ada nilai negatif pada jarak antar titik, apakah langsung dilakukan perhitungan mencari jarak terpendek dengan algoritma dijkstra? Terimakasih min ditunggu kali jawabannya ??
Menurut pemahaman yang saya ketahui mengenai algoritma ini, kesimpulan saya sama dengan kesimpulan anda, yaitu perhitungan langsung dilakukan dengan Algoritma Dijkstra. Untuk dapat tetap menggunakan algoritma ini, perlu diingat bahwa nilai diantara 2 titik tidak selalu diukur menggunakan nliai yang pasti bernilai positif (misalnya jarak), tetapi bisa juga diukur menggunakan nilai yang tidak selalu positif (misalnya biaya, poin, dan lain-lain)
Saya mau tanya min. Kala langsung menggunakan algoritma Djikstra, apakah masih bisa dikatakan menggunakan algoritma Johnson?
Terimakasih
Menurut saya sudah tidak bisa dikatakan seperti itu karena kedua hal ini adalah algoritma yang berbeda. Silahkan menggunakan Algoritma Dijkstra apabila tujuan anda memang menggunakan algoritma tersebut.