Algoritma MSO (Multi Swarm Optimization) adalah salah satu algoritma optimasi yang dapat digunakan untuk pengambilan keputusan, tetapi bisa juga digunakan untuk pencarian jalur. Contoh yang dibahas kali ini adalah mengenai pencarian posisi dengan pengembalian nilai fungsi minimal. .
Multi Swarm Optimization berdasarkan pada Algoritma PSO (Particle Swarm Optimization), dengan perbedaan adalah penggunaan beberapa sub-swarm dibandingkan dengan cara normal yang hanya 1 swarm. Setiap swarm nantinya berfokus pada daerah sendiri-sendiri dan tetap dipengaruhi oleh variabel tertentu yang hanya mempengaruhi tiap swarm. Algoritma ini cocok digunakan untuk optimasi solusi yang memiliki lebih dari 1 solusi pada daerah yang tidak berdekatan.
Diasumsikan ada sebaran titik 3 dimensi, yaitu dimensi x, y, z
Masing-masing dimensi memiliki sebuah konstanta dan batas rentang titik yang dapat digunakan
Contoh data pada masing-masing dimensi adalah sebagai berikut
| Dimensi | konstanta | batas minimal | batas maksimal |
|---|---|---|---|
| x | 3.2 | 10 | 50 |
| y | 3 | 30 | 80 |
| z | 2.5 | 50 | 150 |
Contoh data awal adalah sebagai berikut:
Dim data(2)() As Double
data(0) = New Double() {3.2, 10, 50}
data(1) = New Double() {3, 30, 80}
data(2) = New Double() {2.5, 50, 150}
Nilai fungsi yang diketahui adalah dengan rumus f(x, y, z) = (kx * x^2) + (ky * y^2) + (kz * z^2)
Tentukan posisi dimana fungsi tersebut mengembalikan nilai minimal
Dengan batasan nilai bahwa x + y + z harus bernilai 210
Sebelum masuk kedalam langkah-langkah pembahasan algoritma, ada beberapa konstanta atau parameter yang harus diketahui, yaitu:
* Tentukan dimensi permasalahan
Diasumsikan dalam kasus ini, dimensi bernilai 3 karena ada 3 dimensi yang akan dicari solusinya
Const dimensi As Integer = 3
* Tentukan jumlah partikel yang digunakan dalam perhitungan
Diasumsikan dalam kasus ini, jumlah partikel yang digunakan adalah 4 partikel
Dim jumlahPartikel As Integer = 4
* Tentukan jumlah swarm yang digunakan dalam perhitungan
Diasumsikan dalam kasus ini, jumlah swarm yang digunakan adalah 3 swarm
Dim jumlahSwarm As Integer = 3
* Tentukan jumlah iterasi yang digunakan oleh setiap partikel untuk melakukan proses
Diasumsikan dalam kasus ini, jumlah iterasi yang digunakan adalah 50 kali
Dim jumlahIterasi As Integer = 50
* Tentukan total posisi yang harus dicapai
Semua solusi yang ditemukan oleh masing-masing individu harus berjumlah sebanyak variabel ini
Diasumsikan dalam kasus ini, total nilai yang harus dicapai adalah 210
Const totalPosisi As Integer = 210
* Tentukan batas kecepatan untuk perpindahan posisi partikel dalam setiap proses
Diasumsikan dalam kasus ini nilai minimal dan nilai maksimal adalah 10% dari masing-masing batas nilai pada tiap-tiap dimensi
Sebagai contoh kasus, apabila nilai minimal dan maksimal dari sebuah dimensi adalah 10 dan 50,
Maka nilai minimalnya adalah -(50-10)/10 = -4, dan nilai maksimalnya adalah (50-10)/10 = 4
Dim minKecepatan(dimensi - 1) As Double Dim maksKecepatan(dimensi - 1) As Double For i As Integer = 0 To dimensi - 1 minKecepatan(i) = -(data(i)(2) - data(i)(1)) / 10 maksKecepatan(i) = (data(i)(2) - data(i)(1)) / 10 Next
Langkah-langkah penggunaan algoritma ini adalah
1. Inisialisasi semua komponen yang dibutuhkan dalam perhitungan, yaitu partikel, swarm, dan multiswarm
Buat matriks Multiswarm sebanyak variabel jumlahSwarm
Buat matriks Swarm sebanyak variabel jumlahPartikel, dan masukkan masing-masing Swarm ke dalam matriks MultiSwarm
Buat partikel sebanyak variabel jumlahSwarm * jumlahPartikel, dan masukkan masing-masing Partikel ke dalam matriks Swarm
Beri nilai posisi partikel awal dengan posisi acak
Kemudian cari nilai fitness nya
Ambil posisi terbaik sementara berdasarkan nilai fitness tertinggi sementara
Penjelasan lebih detail tentang fungsi ini dapat dilihat pada penjelasan skrip dibawah ini
Dim ms As New Multiswarm(jumlahSwarm, jumlahPartikel, dimensi, minKecepatan, maksKecepatan, totalPosisi, data)
* Agar dapat menjalankan skrip diatas, maka diperlukan beberapa Class, yaitu Class Multiswarm, Class Swarm, dan Class Partikel.
Class Partikel berisi data posisi, kecepatan, dan nilai fitness partikel tersebut
Class Swarm berisi data partikel beserta posisi dan nilai fitness terbaik pada swarm tersebut
Class MultiSwarm berisi data swarm beserta posisi dan nilai fitness terbaik pada swarm tersebut
Deklarasi masing-masing Class adalah sebagai berikut:
Public Class Partikel
Private Shared rnd As New Random(0)
Public posisi() As Integer
Public kecepatan() As Double
Public fitness As Double
Public posisiPartikelTerbaik() As Integer
Public fitnessPartikelTerbaik As Double
Public Sub New(ByVal dimensi As Integer, ByVal totalPosisi As Integer, ByVal data()() As Double)
posisi = New Integer(dimensi - 1) {}
kecepatan = New Double(dimensi - 1) {}
posisiPartikelTerbaik = New Integer(dimensi - 1) {}
Dim jumlahPosisi As Integer = 0
Do While jumlahPosisi <> totalPosisi
'Inisialisasi semua posisi partikel awal dengan posisi acak
'Setiap dimensi memiliki batas minimal dan maksimal sendiri-sendiri, sesuai pada isian parameter data
jumlahPosisi = 0
For i As Integer = 0 To posisi.Length - 1
posisi(i) = rnd.Next(data(i)(1), data(i)(2))
jumlahPosisi += posisi(i)
Next
'Perlu diingat bahwa jumlah posisi diatas belum tentu sesuai dengan parameter totalPosisi
'Oleh karena itu, lakukan penyesuaian posisi agar jumlah posisi selalu bernilai sama dengan parameter totalPosisi
Dim selisih As Integer = totalPosisi - jumlahPosisi
Dim idx As Integer = rnd.Next(dimensi)
Dim posisiBaru As Integer = posisi(idx) + selisih
If posisiBaru < data(idx)(1) Then Continue Do
If posisiBaru > data(idx)(2) Then Continue Do
jumlahPosisi = jumlahPosisi - posisi(idx) + posisiBaru
posisi(idx) = posisiBaru
Loop
'Inisialisasi nilai kecepatan semua partikel awal dengan nilai kecepatan acak
For j As Integer = 0 To kecepatan.Length - 1
Dim lo As Double = -1.0 * Math.Abs(data(j)(2) - data(j)(1)) / 10
Dim hi As Double = Math.Abs(data(j)(2) - data(j)(1)) / 10
kecepatan(j) = (hi - lo) * rnd.NextDouble() + lo
Next j
'Hitung nilai fitness dari posisi acak tersebut
'Karena tujuan permasalahan adalah mencari nilai minimal, maka semakin rendah nilai fungsi akan semakin baik
'Penjelasan lebih detail tentang fungsi ini dapat dilihat pada penjelasan skrip dibawah ini
fitness = HitungFitness(posisi, data)
fitnessPartikelTerbaik = fitness
Array.Copy(posisi, posisiPartikelTerbaik, dimensi)
End Sub
. . .
End Class
Public Class Swarm
Public daftarPartikel() As Partikel
Public posisiSwarmTerbaik() As Integer
Public fitnessSwarmTerbaik As Double
Public Sub New(ByVal jumlahPartikel As Integer, ByVal dimensi As Integer, ByVal totalPosisi As Integer, ByVal data()() As Double)
fitnessSwarmTerbaik = Double.MaxValue
posisiSwarmTerbaik = New Integer(dimensi - 1) {}
daftarPartikel = New Partikel(jumlahPartikel - 1) {}
For i = 0 To daftarPartikel.Length - 1
daftarPartikel(i) = New Partikel(dimensi, totalPosisi, data)
If daftarPartikel(i).fitness < fitnessSwarmTerbaik Then
fitnessSwarmTerbaik = daftarPartikel(i).fitness
Array.Copy(daftarPartikel(i).posisi, posisiSwarmTerbaik, dimensi)
End If
Next i
End Sub
. . .
End Class
Public Class Multiswarm
Public daftarSwarm() As Swarm
Public posisiMultiSwarmTerbaik() As Integer
Public fitnessMultiSwarmTerbaik As Double
Public dimensi As Integer
Public minKecepatan() As Double
Public maksKecepatan() As Double
Public totalPosisi As Integer
Public data()() As Double
Private Shared rnd As New Random(0)
Public Sub New(ByVal jumlahSwarm As Integer, ByVal jumlahPartikel As Integer, ByVal dimensi As Integer, ByVal minKecepatan() As Double, ByVal maksKecepatan() As Double, ByVal totalPosisi As Integer, ByVal data()() As Double)
daftarSwarm = New Swarm(jumlahSwarm - 1) {}
posisiMultiSwarmTerbaik = New Integer(dimensi - 1) {}
fitnessMultiSwarmTerbaik = Double.MaxValue
Me.dimensi = dimensi
Me.minKecepatan = minKecepatan
Me.maksKecepatan = maksKecepatan
Me.totalPosisi = totalPosisi
Me.data = data
For i = 0 To jumlahSwarm - 1
daftarSwarm(i) = New Swarm(jumlahPartikel, dimensi, totalPosisi, data)
If daftarSwarm(i).fitnessSwarmTerbaik < fitnessMultiSwarmTerbaik Then
fitnessMultiSwarmTerbaik = daftarSwarm(i).fitnessSwarmTerbaik
Array.Copy(daftarSwarm(i).posisiSwarmTerbaik, posisiMultiSwarmTerbaik, dimensi)
End If
Next i
End Sub
. . .
End Class
* Gunakan fungsi ini untuk menghitung nilai fitness pada masing-masing partikel
Rumus yang digunakan adalah sesuai dengan rumus yang sudah ditentukan, yaitu
f(x, y, z) = (kx * x^2) + (ky * y^2) + (kz * z^2)
Public Function HitungFitness(ByVal posisi() As Integer, ByVal data()() As Double) As Double Dim hasil As Double = 0.0 For i As Integer = 0 To posisi.Length - 1 hasil += data(i)(0) * posisi(i) * posisi(i) Next i Return hasil End Function
2. Lakukan proses pencarian posisi terbaik sebanyak jumlah perulangan
Penjelasan lebih detail tentang fungsi ini dapat dilihat pada penjelasan skrip dibawah ini (poin 2a – 2d)
ms.prosesPencarianPosisi(jumlahIterasi)
2a. Tentukan bobot inertia (w), bobot kognitif (c1), bobot sosial (c2), dan bobot global (c3)
Nilai acuan untuk masing-masing variabel dapat dilihat di http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=00870279
Diasumsikan dalam kasus ini, nilai bobot tersebut akan mengikuti nilai acuan yang sudah ada
Const w As Double = 0.729 Const c1 As Double = 1.49445 Const c2 As Double = 1.49445 Const c3 As Double = 0.3645
2b. Tentukan probabilitas sebuah partikel akan dibuang dan dibuat ulang
Diasumsikan dalam kasus ini, nilai probabilitas tersebut adalah 0.005
Const probBuatBaru As Double = 0.005
2c. Tentukan probabilitas sebuah partikel akan bertukar dengan partikel acak dalam swarm acak
Diasumsikan dalam kasus ini, nilai probabilitas tersebut adalah 0.005
Const probTukarPartikel As Double = 0.005
2d. Lakukan proses pencarian posisi terbaik sebanyak jumlah perulangan (poin 2d1 – 2d9)
2d1. Lakukan perulangan untuk setiap partikel
Cari angka acak antara 0 sampai dengan 1
Jika angka acak termasuk dalam probabilitas pembuangan partikel, maka lakukan pembuangan dan buat ulang partikel tersebut
Dim p As Double = rnd.NextDouble If p < probBuatBaru Then daftarSwarm(i).daftarPartikel(j) = New Partikel(dimensi, totalPosisi, data) End If
2d2. Cari angka acak antara 0 sampai dengan 1
Jika angka acak termasuk dalam probabilitas pertukaran partikel, maka lakukan pertukaran partikel
Partikel akan ditukar dengan partikel acak dalam swarm acak
Dim q As Double = rnd.NextDouble If q < probTukarPartikel Then Dim swarmAcak As Integer = rnd.Next(0, daftarSwarm.Length) Dim partikelAcak As Integer = rnd.Next(0, daftarSwarm(0).daftarPartikel.Length) Dim tmp As Partikel = daftarSwarm(i).daftarPartikel(j) daftarSwarm(i).daftarPartikel(j) = daftarSwarm(swarmAcak).daftarPartikel(partikelAcak) daftarSwarm(swarmAcak).daftarPartikel(partikelAcak) = tmp End If
2d3. Cari kecepatan perpindahan posisi yang baru dengan rumus:
v baru = (w * v skrg) + (c1 * r1 * (posisi partikel terbaik – posisi partikel skrg)) + (c2 * r2 * (posisi swarm terbaik – posisi partikel skrg) + (c3 * r3 * (posisi multiswarm terbaik – posisi partikel skrg))
Jika kecepatan yang baru ternyata diluar batas variabel minKecepatan dan maksKecepatan (-1 s/d 1), maka kembalikan kecepatan agar masuk dalam batas
For k = 0 To dimensi - 1 Dim r1 As Double = rnd.NextDouble Dim r2 As Double = rnd.NextDouble Dim r3 As Double = rnd.NextDouble daftarSwarm(i).daftarPartikel(j).kecepatan(k) = (w * daftarSwarm(i).daftarPartikel(j).kecepatan(k)) + (c1 * r1 * (daftarSwarm(i).daftarPartikel(j).posisiPartikelTerbaik(k) - daftarSwarm(i).daftarPartikel(j).posisi(k))) + (c2 * r2 * (daftarSwarm(i).posisiSwarmTerbaik(k) - daftarSwarm(i).daftarPartikel(j).posisi(k))) + (c3 * r3 * (posisiMultiSwarmTerbaik(k) - daftarSwarm(i).daftarPartikel(j).posisi(k))) If daftarSwarm(i).daftarPartikel(j).kecepatan(k) < minKecepatan(k) Then daftarSwarm(i).daftarPartikel(j).kecepatan(k) = minKecepatan(k) ElseIf daftarSwarm(i).daftarPartikel(j).kecepatan(k) > maksKecepatan(k) Then daftarSwarm(i).daftarPartikel(j).kecepatan(k) = maksKecepatan(k) End If Next k
2d4. Lakukan update posisi yang baru dengan cara posisi lama + kecepatan baru
Jika posisi yang baru ternyata diluar batas variabel minX dan maksX (0 – 5), maka kembalikan posisinya agar masuk dalam batas
Dim posisiBaru(dimensi - 1) As Integer For k = 0 To dimensi - 1 posisiBaru(k) = daftarSwarm(i).daftarPartikel(j).posisi(k) + daftarSwarm(i).daftarPartikel(j).kecepatan(k) If posisiBaru(k) < data(k)(1) Then posisiBaru(k) = data(k)(1) ElseIf posisiBaru(k) > data(k)(2) Then posisiBaru(k) = data(k)(2) End If Next k
2d5. Sama seperti perhitungan sebelumnya, jumlah posisi yang baru belum tentu sesuai dengan parameter totalPosisi
Oleh karena itu, lakukan penyesuaian posisi agar jumlah posisi selalu bernilai sama dengan parameter totalPosisi
Dim jumlahPosisi As Integer = 0 For k As Integer = 0 To dimensi - 1 jumlahPosisi += posisiBaru(k) Next Do While jumlahPosisi <> totalPosisi Dim selisih As Integer = totalPosisi - jumlahPosisi Dim selisihPerDimensi(dimensi - 1) As Integer Dim idx As Integer = -1 Do While selisih <> 0 idx = rnd.Next(dimensi) If selisih > 0 Then If posisiBaru(idx) + selisihPerDimensi(idx) < data(idx)(2) Then selisihPerDimensi(idx) += 1 selisih -= 1 End If Else If posisiBaru(idx) + selisihPerDimensi(idx) > data(idx)(1) Then selisihPerDimensi(idx) -= 1 selisih += 1 End If End If Loop For k As Integer = 0 To dimensi - 1 Dim posBaru As Integer = posisiBaru(k) + selisihPerDimensi(k) If posBaru < data(k)(1) Then Continue Do If posBaru > data(k)(2) Then Continue Do Next For k As Integer = 0 To dimensi - 1 Dim posBaru As Integer = posisiBaru(k) + selisihPerDimensi(k) jumlahPosisi = jumlahPosisi - posisiBaru(k) + posBaru posisiBaru(k) = posBaru Next Loop posisiBaru.CopyTo(daftarSwarm(i).daftarPartikel(j).posisi, 0)
2d6. Hitung nilai fitness untuk posisi yang baru
daftarSwarm(i).daftarPartikel(j).fitness = HitungFitness(daftarSwarm(i).daftarPartikel(j).posisi, data)
2d7. Jika nilai fitness baru lebih baik dari nilai fitness yang diperoleh partikel tersebut sebelumnya, maka ambil posisi yang baru sebagai posisi terbaik partikel tersebut
If daftarSwarm(i).daftarPartikel(j).fitness < daftarSwarm(i).daftarPartikel(j).fitnessPartikelTerbaik Then daftarSwarm(i).daftarPartikel(j).fitnessPartikelTerbaik = daftarSwarm(i).daftarPartikel(j).fitness Array.Copy(daftarSwarm(i).daftarPartikel(j).posisi, daftarSwarm(i).daftarPartikel(j).posisiPartikelTerbaik, dimensi) End If
2d8. Jika nilai fitness baru ternyata lebih baik dari nilai fitness swarm partikel tersebut, maka ambil posisi yang baru sebagai posisi terbaik swarm partikel tersebut
If daftarSwarm(i).daftarPartikel(j).fitness < daftarSwarm(i).fitnessSwarmTerbaik Then daftarSwarm(i).fitnessSwarmTerbaik = daftarSwarm(i).daftarPartikel(j).fitness Array.Copy(daftarSwarm(i).daftarPartikel(j).posisi, daftarSwarm(i).posisiSwarmTerbaik, dimensi) End If
2d9. Jika nilai fitness baru ternyata lebih baik dari nilai fitness umum, maka ambil posisi yang baru sebagai posisi terbaik secara umum
If daftarSwarm(i).daftarPartikel(j).fitness < fitnessMultiSwarmTerbaik Then fitnessMultiSwarmTerbaik = daftarSwarm(i).daftarPartikel(j).fitness Array.Copy(daftarSwarm(i).daftarPartikel(j).posisi, posisiMultiSwarmTerbaik, dimensi) End If
Hasil akhir adalah: (klik untuk perbesar gambar)
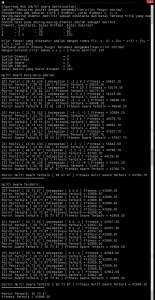
Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:
[sdm_download id=”650″ fancy=”0″]
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.

Bagaimana cara debug atau menjalankan program anda?
File yang saya bagikan adalah skrip bertipe konsol. Setelah anda menjalankan Visual Studio, silahkan membuat proyek baru dengan tipe “Console Application”, kemudian salin isi skrip pada file yang disediakan atau anda bisa menimpa langsung modul kosong pada proyek tersebut.
siang min, kontennya manarik, mau tanya kalau penerapan algoritma sepeti ini untuk aplikasi seperti rapid minner / weka penggunaannya ada tutorialnya gak min,?
Mohon maaf saya tidak menyediakan tutorial seperti itu.
malam min
pada contoh kasus admin diatas menggunakan satu fungsi yaitu f(x, y, z) = (kx * x^2) + (ky * y^2) + (kz * z^2)
jika kasusnya ada tiga variable [v f a]
LB[130 0.151.5]
UB[140 0.2 2.0]
fungsinya ada 4
VB = 0.166 + 0.017 v + 0.135 f + 0.015 a
tc = 94.1 – 0.32 v – 14 f – 5.06 a
Ra = – 3.98 + 0.0228 v + 8.65 f + 0.745 a
VMR = 24 – 13.2 v – 16 f + 77.4 a
mohon pencerahannya min
bagaimana cara menghitung ke empat fungsi tersebut sekalian
Jika perhitungan fungsi menggunakan lebih dari 1 fungsi, maka harus diketahui tujuan apakah yang ingin anda cari pada permasalahan tersebut. Apakah dari keempat fungsi tersebut terhubung satu sama lain, ataukah ada urutan prioritas, ataukah ada fungsi yang bergantung dan tidak bergantung pada fungsi lainnya, ataukah ada kondisi tambahan lainnya sehubungan dengan keempat fungsi tersebut. Silahkan coba diceritakan secara lebih lanjut.
Permisi min, ada no hp yang bisa dihubungi ? saya mau diskusi mengenai algoritma elgamal lebih lanjut. terima kasih.
Silahkan menghubungi kami dengan nomor kontak yang tersedia pada halaman hubungi kami https://piptools.net/hubungi-kami/
dari fungsi Vb, Tc, Ra dan VMR
secara simultan digunakan dalam simulasi untuk mendapatkan VMR optimumnya pada keadaan Vb, Tc dan Ra yang dapat diterima
terimakasih banyak min
Sebelumnya anda sampaikan mengenai “VMR optimum” tetapi jika saya melihat kembali rumus diatas, fungsi VMR hanya bergantung pada variabel v, f dan a dan tidak memiliki ikatan dengan Vb, Tc dan Ra. Jika optimum tersebut bergantung “pada keadaan Vb, Tc dan Ra yang dapat diterima” maka harus ada keterikatan antara rumus VMR dengan ketiga fungsi lainnya.
Maaf mau tanya, apakah ada rumus per step by step dari multi swarm optimization ini?
Algoritma Multi swarm bisa dikatakan sebagai upgrade atau peningkatan dari algoritma PSO (Particle Swarm Optimization), dimana algoritma tersebut, dan sama seperti kebanyakan algoritma optimasi pada umumnya, tidak memiliki rumus baku karena implementasi algoritma akan menyesuaikan studi kasus yang tersedia.
maaf mau tanya, apakah algoritma ini dapat diterapkan untuk pemilihan base station dan sensor node pada protocol routing wsn?
Jika permasalahan pada topik tersebut membutuhkan pemecahan masalah yang bersifat optimasi, maka seharusnya algoritma ini dapat diterapkan.