Algoritma AMO (Amoeba Method Optimization) / Nelder-Mead Method adalah salah satu algoritma optimasi yang dapat digunakan untuk pengambilan keputusan. Contoh yang dibahas kali ini adalah mengenai pencarian posisi dengan pengembalian nilai fungsi maksimal.
Amoeba Method Optimization, atau disebut juga dengan Nelder-Mead Method dan Simplex Optimization, adalah metode numerik umum yang digunakan untuk mencari nilai minimal atau maksimal dari sebuah fungsi obyektif pada ruang multi dimensi. Simplex Optimization bekerja dengan cara membentuk segitiga solusi yang dikatakan sebagai solusi terbaik – lainnya – terburuk. Pada setiap perhitungan, segitiga ini akan dihitung sehingga semakin mendekati solusi yang terbaik. Apabila segitiga ini digambar secara berurutan pada setiap perulangan, gerakan segitiga yang terjadi mirip dengan pola gerakan Amoeba.
Diasumsikan ada sebaran titik 2 dimensi antara -2 sampai dengan 2
Fungsi yang diketahui adalah fungsi Himmelblau, dengan rumus f(x, y) = (x^2+y-11)^2 + (x+y^2-7)^2
Tentukan posisi dimana fungsi tersebut mengembalikan nilai maksimal
Fungsi Himmelblau adalah salah satu fungsi yang dapat digunakan untuk mengoptimasi suatu permasalahan. Fungsi ini memiliki sebuah nilai maksimum pada x = -0.270845, and y = -0.923039 dengan nilai fungsi sebesar f(x,y) = 181.617, dengan asumsi bahwa rentang minimal dan maksimal dari sebaran titik adalah -2 sampai dengan 2
Grafik fungsi Himmelblau yang normal, atau untuk sebaran titik tak terbatas adalah sebagai berikut.
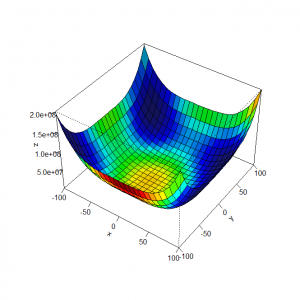
Sedangkan Grafik fungsi Himmelblau untuk sebaran titik dengan rentang minimal -2 dan maksimal 2 adalah sebagai berikut.
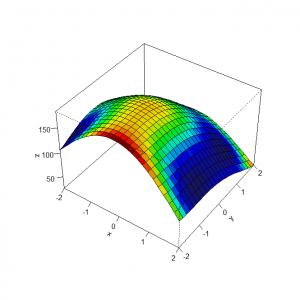
Dapat dilihat bahwa pada gambar tersebut, didapatkan area dengan titik tertinggi (berwarna merah) berada pada area x = -0, and y = -1, dimana titik tersebut mengembalikan nilai fungsi tertinggi. Oleh sebab itu digunakan algoritma ini untuk mencari titik di area berwarna merah tersebut.
* Tentukan jumlah Amoeba yang digunakan dalam perhitungan
Jumlah amoeba harus minimal 3 buah, dengan batas maksimal tidak ada
Semakin banyak amoeba yang digunakan, semakin akurat nilai akhirnya, tetapi semakin lama proses perhitungannya
Diasumsikan dalam kasus ini, jumlah amoeba ada 5 buah
Dim jumlahAmoeba As Integer = 5
* Tentukan posisi minimal dan maksimal dari fungsi yang akan dihitung
Jika tidak ada batasan posisi, tentu saja posisi yang mendekati tak terhingga akan terpilih karena akan mengembalikan nilai fungsi yang sangat besar
Diasumsikan dalam kasus ini, posisi minimal adalah -2, dan posisi maksimal adalah +2
Dim minPosisi As Double = -2 Dim maksPosisi As Double = +2
* Tentukan jumlah iterasi yang digunakan dalam perhitungan
Diasumsikan dalam kasus ini, jumlah iterasi adalah 50 kali
Dim jumlahIterasi As Integer = 50
Langkah-langkah penggunaan algoritma ini adalah
1. Inisialisasi nilai awal untuk semua amoeba
Beri posisi acak untuk tiap-tiap amoeba
Kemudian hitung nilai fungsi untuk posisi acak tersebut
Dim amoeba As New Amoeba(jumlahAmoeba, dimensi, minPosisi, maksPosisi, jumlahIterasi)
* Agar dapat menjalankan skrip diatas, maka diperlukan sebuah Class Amoeba untuk menampung semua data solusi yang diperoleh amoeba tersebut. Deklarasi Class Amoeba adalah sebagai berikut:
Public Class Amoeba
Public jumlahAmoeba As Integer
Public dimensi As Integer
Public daftarSolusi() As Solusi
Public minPosisi As Double
Public maksPosisi As Double
Public alpha As Double 'Koefisien untuk menghitung nilai reflected
Public beta As Double 'Koefisien untuk menghitung nilai contracted
Public gamma As Double 'Koefisien untuk menghitung nilai expanded
Public jumlahIterasi As Integer
Public Sub New(ByVal jumlahAmoeba As Integer, ByVal dimensi As Integer, ByVal minPosisi As Double, ByVal maksPosisi As Double, ByVal jumlahIterasi As Integer)
Me.jumlahAmoeba = jumlahAmoeba
Me.dimensi = dimensi
Me.minPosisi = minPosisi
Me.maksPosisi = maksPosisi
Me.alpha = 1.0 'didapatkan dari teori jurnal penelitian
Me.beta = 0.5 'didapatkan dari teori jurnal penelitian
Me.gamma = 2.0 'didapatkan dari teori jurnal penelitian
Me.jumlahIterasi = jumlahIterasi
Me.daftarSolusi = New Solusi(jumlahAmoeba - 1) {}
For i = 0 To daftarSolusi.Length - 1
daftarSolusi(i) = New Solusi(dimensi, minPosisi, maksPosisi)
Next i
'Perlu diingat bahwa, setelah proses pengurutan maka
'daftarSolusi(0) adalah merupakan posisi terbaik
'daftarSolusi(n-1) adalah merupakan posisi terburuk
Array.Sort(daftarSolusi)
End Sub
. . .
End Class
2. Lakukan proses pencarian posisi terbaik sebanyak jumlah iterasi
Penjelasan lebih detail tentang fungsi ini dapat dilihat pada penjelasan skrip dibawah ini (poin 2a – 2e)
Dim solusi As Solusi = amoeba.ProsesPerhitungan
Sedikit pembahasan sebelum memasuki perhitungan utama
Dalam setiap kali perulangan, metode ini akan mencari nilai centroid, reflected, expanded, contracted
Untuk hal tersebut akan digunakan 4 fungsi tambahan untuk menghitung nilai-nilai tersebut
Penjelasan untuk masing-masing nilai tersebut adalah sebagai berikut:
Gunakan fungsi ini untuk mencari nilai centroid
Centroid adalah nilai rata-rata dari semua posisi kecual posisi terburuk
Public Function Centroid() As Solusi Dim c(dimensi - 1) As Double For i = 0 To jumlahAmoeba - 2 For j = 0 To dimensi - 1 c(j) += daftarSolusi(i).matriks(j) Next j Next i For j = 0 To dimensi - 1 c(j) = c(j) / (jumlahAmoeba - 1) If c(j) < minPosisi Then c(j) = minPosisi ElseIf c(j) > maksPosisi Then c(j) = maksPosisi End If Next j Dim s As New Solusi(c) 'Buat solusi baru pada posisi ini, dan hitung nilai fungsinya Return s End Function
Gunakan 3 fungsi dibawah ini untuk mencari nilai reflected, expanded, contracted
Ilustrasi singkat adalah sebagai berikut:
b----------x----------c----------y----------z
buruk-----------------centroid
Tarik garis lurus antara posisi terburuk dengan posisi centroid
Kemudian tambahkan garis terusan dari posisi centroid sepanjang jarak sebelumnnya
Posisi Reflected berada pada posisi y, dengan jarak (centroid-buruk) * koefisien alpha, dalam contoh ini bernilai 1.0
Posisi Expanded berada pada posisi z, dengan jarak (centroid-buruk) * koefisien gamma, dalam contoh ini bernilai 2.0
Posisi Contracted berada pada posisi x, dengan jarak (centroid-buruk) * koefisien beta, dalam contoh ini bernilai 0.5
Public Function Reflected(ByVal centroid As Solusi) As Solusi Dim r(dimensi - 1) As Double Dim terburuk() As Double = Me.daftarSolusi(jumlahAmoeba - 1).matriks For j = 0 To dimensi - 1 r(j) = ((1 + alpha) * centroid.matriks(j)) - (alpha * terburuk(j)) If r(j) < minPosisi Then r(j) = minPosisi ElseIf r(j) > maksPosisi Then r(j) = maksPosisi End If Next j Dim s As New Solusi(r) Return s End Function Public Function Expanded(ByVal reflected As Solusi, ByVal centroid As Solusi) As Solusi Dim e(dimensi - 1) As Double For j = 0 To dimensi - 1 e(j) = (gamma * reflected.matriks(j)) + ((1 - gamma) * centroid.matriks(j)) If e(j) < minPosisi Then e(j) = minPosisi ElseIf e(j) > maksPosisi Then e(j) = maksPosisi End If Next j Dim s As New Solusi(e) Return s End Function Public Function Contracted(ByVal centroid As Solusi) As Solusi Dim v(dimensi - 1) As Double Dim terburuk() As Double = Me.daftarSolusi(jumlahAmoeba - 1).matriks For j = 0 To dimensi - 1 v(j) = (beta * terburuk(j)) + ((1 - beta) * centroid.matriks(j)) If v(j) < minPosisi Then v(j) = minPosisi ElseIf v(j) > maksPosisi Then v(j) = maksPosisi End If Next j Dim s As New Solusi(v) Return s End Function
Kembali pada proses pencarian posisi terbaik oleh fungsi ProsesPerhitungan (poin 2) yang sudah disebutkan diatas
2a. Hitung nilai centroid, kemudian hitung nilai reflected
Dim centroid As Solusi = Me.Centroid Dim reflected As Solusi = Me.Reflected(centroid)
2b. Jika nilai reflected lebih baik dari nilai solusi terbaik, maka hitung nilai expanded
Jika nilai expanded ternyata lebih baik dari nilai reflected, maka update posisi terburuk dengan posisi expanded
Jika nilai expanded ternyata tidak lebih baik dari nilai reflected, maka update posisi terburuk dengan posisi reflected
If reflected.nilai > daftarSolusi(0).nilai Then
Dim expanded As Solusi = Me.Expanded(reflected, centroid)
If expanded.nilai > daftarSolusi(0).nilai Then
Console.WriteLine("Posisi expanded baru ditemukan: " & expanded.ToString)
UpdatePosisiTerburuk(expanded)
Else
Console.WriteLine("Posisi reflected baru ditemukan: " & reflected.ToString)
UpdatePosisiTerburuk(reflected)
End If
Continue Do
End If
2c. Tentukan apakah nilai reflected ternyata paling buruk (nilai terendah) dari semua nilai selain nilai posisi terburuk
Dim IsTerendahSelainTerburuk As Boolean = True For i = 0 To jumlahAmoeba - 2 If reflected.nilai > daftarSolusi(i).nilai Then 'Ternyata ada yang nilai nya lebih buruk dari nilai reflected IsTerendahSelainTerburuk = False Exit For End If Next i
2d. Jika benar nilai reflected ternyata paling buruk (nilai terendah) dari semua nilai selain nilai posisi terburuk, maka:
– Jika nilai reflected ternyata masih lebih baik dari nilai solusi terburuk, maka update posisi terburuk dengan posisi reflected
– Hitung nilai contracted
– Jika nilai contracted ternyata lebih baik dari nilai solusi terburuk, maka update posisi terburuk dengan posisi contracted
– Jika nilai contracted ternyata tidak lebih baik dari nilai solusi terburuk, maka solusi baru tidak ditemukan
Jika solusi baru tidak ditemukan maka lakukan proses perpindahan semua posisi kecual posisi terbaik
Posisi baru untuk masing-masing posisi adalah setengah jarak dari (posisi terbaik dan posisi tersebut), kemudian hitung nilai fungsi baru untuk masing-masing posisi
If IsTerendahSelainTerburuk Then
If reflected.nilai > daftarSolusi(jumlahAmoeba - 1).nilai Then
UpdatePosisiTerburuk(reflected)
End If
Dim contracted As Solusi = Me.Contracted(centroid)
If contracted.nilai > daftarSolusi(0).nilai Then
Console.WriteLine("Posisi contracted baru ditemukan: " & contracted.ToString)
End If
If contracted.nilai > daftarSolusi(jumlahAmoeba - 1).nilai Then
UpdatePosisiTerburuk(contracted)
Else
For i = 1 To jumlahAmoeba - 1
For j = 0 To dimensi - 1
daftarSolusi(i).matriks(j) = (daftarSolusi(i).matriks(j) + daftarSolusi(0).matriks(j)) / 2.0
daftarSolusi(i).nilai = hitungFungsi(daftarSolusi(i).matriks)
Next j
Next i
Array.Sort(daftarSolusi)
End If
Continue Do
End If
2e. Lakukan perhitungan poin 2a – 2d sebanyak jumlah iterasi
* Agar dapat menjalankan skrip diatas, maka diperlukan sebuah Class Solusi untuk menampung semua data posisi beserta nilai fungsinya. Deklarasi Class Solusi adalah sebagai berikut:
Public Class Solusi
Implements IComparable(Of Solusi)
Public matriks() As Double 'Posisi
Public nilai As Double 'Nilai fungsi posisi tersebut
Private Shared random As New Random(1)
Public Sub New(ByVal dimensi As Integer, ByVal minPosisi As Double, ByVal maksPosisi As Double)
'Membuat matriks baru dengan nilai posisi acak
Me.matriks = New Double(dimensi - 1) {}
For i = 0 To dimensi - 1
Me.matriks(i) = (maksPosisi - minPosisi) * random.NextDouble + minPosisi
Next i
Me.nilai = hitungFungsi(Me.matriks)
End Sub
Public Sub New(ByVal matriks() As Double)
'Membuat matriks baru dengan nilai posisi tertentu
Me.matriks = New Double(matriks.Length - 1) {}
Array.Copy(matriks, Me.matriks, matriks.Length)
Me.nilai = hitungFungsi(Me.matriks)
End Sub
Public Function CompareTo(ByVal other As Solusi) As Integer Implements IComparable(Of Solusi).CompareTo
If Me.nilai < other.nilai Then
Return 1
ElseIf Me.nilai > other.nilai Then
Return -1
Else
Return 0
End If
End Function
Public Overrides Function ToString() As String
Dim s As String = "["
For i = 0 To Me.matriks.Length - 1
If matriks(i) >= 0.0 Then
s &= " "
End If
s &= " " & matriks(i).ToString("F2")
Next i
s &= "] nilai fungsi = " & Me.nilai.ToString("F4")
Return s
End Function
End Class
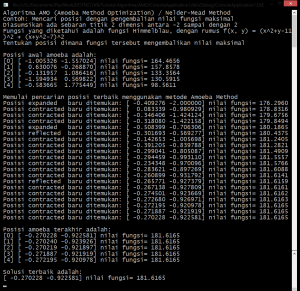
Hasil akhir adalah: (klik untuk perbesar gambar)
Dapat dilihat bahwa hasil akhir perhitungan tidak sama dengan x = -0.270845, and y = -0.923039, tetapi sangat mendekati posisi tersebut. Jika ingin mendapatkan jawaban yang lebih mirip lagi, maka silahkan lakukan penambahan jumlah iterasi, dengan resiko bahwa perhitungan yang dilakukan akan semakin lama.
Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:
[sdm_download id=”641″ fancy=”0″]
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.

Leave a Reply