Algoritma BWT (Berkeley Wavelet Transform) adalah salah satu algoritma yang dapat digunakan untuk melakukan kompresi sinyal ataupun gambar. Contoh yang dibahas kali ini adalah mengenai pengolahan file gambar.
Sama seperti algoritma transformasi wavelet sebelumnya, algoritma ini akan melakukan konversi data dari bentuk spasial menjadi bentuk frekuensi, kemudian melakukan pengolahan data frekuensi, dan dikonversi menjadi bentuk spasial menggunakan inversi metode yang bersangkutan.
Diketahui data awal adalah sebagai berikut. Dalam kasus ini akan digunakan gambar berwarna bertipe jpg dengan ukuran 128 x 128 pixel

Langkah-langkah penggunaan algoritma ini adalah
1. Lakukan konversi ke dalam bentuk grayscale
Kemudian potong gambar tersebut agar berukuran persegi
Dan lakukan proses downsample kedalam ukuran kelipatan pangkat 3 yang paling mendekati ukuran semula
img = double(img); img = mean(img,3); ukuran = min(size(img)); img = img(1:ukuran,1:ukuran); ukuranBaru = 3^floor(log(ukuran)/log(3)); img = imresize(img,ukuranBaru/ukuran);
2. Lakukan proses perhitungan dengan menggunakan metode BWT (Berkeley Wavelet Transform)
Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah ini (poin 2a – 2b)
imgbwt = bwt(img);
Memasuki perhitungan pada fungsi BWT
2a. Hitung jumlah level dekomposisi yang akan dilakukan, yaitu pangkat dari ukuran gambar
jumlahLevel = log(ukuran)/log(3);
2b. Lakukan perulangan sebanyak jumlah level (poin 2b1 – 2b3)
for level = 1:jumlahLevel . . .
2b1. Lakukan proses dekomposisi gambar pada level yang sedang terpilih
Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah ini (poin 2b1a – 2b1c)
dekomposisiLevel = bwtPerLevel(img);
Memasuki perhitungan pada fungsi bwtPerLevel
2b1a. Hitung jumlah ukuran output dekomposisi pada level yang sedang terhitung
ukuranSisi = ukuran/3;
2b1b. Inisialisasi parameter orientasi untuk digunakan dalam proses filter
Orientasi yang digunakan adalah berukuran 3 x 3, dengan nilai sebagai berikut:
[ 90-odd 135-odd 45-even ]
[ 90-even 135-even 45-odd ]
[ DC 0-even 0 -odd ]
orientasi = [90 0; 135 0; 45 90; ...
90 90; 135 90; 45 0; ...
-1 -1; 0 90; 0 0];
2b1c. Lakukan perhitungan pada masing-masing orientasi tersebut (poin 2b1c1 – 2b1c2)
for i = 1:size(orientasi,1) . . .
2b1c1. Hitung filter wavelet pada orientasi tersebut
Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah ini
filterWavelet = buatWavelet(orientasi(i,1),orientasi(i,2));
* Gunakan fungsi ini untuk menghitung filter wavelet yang digunakan
function filterWavelet = buatWavelet(orientasi,fase)
filterWavelet = nan;
if (orientasi==-1)
filterWavelet = ones(3,3)/sqrt(9);
elseif (orientasi==0)
if (fase==0)
filterWavelet = [-1 0 1; -1 0 1; -1 0 1]/sqrt(6);
elseif (fase==90)
filterWavelet = [-1 2 -1; -1 2 -1; -1 2 -1]/sqrt(18);
end
elseif (orientasi==45)
if (fase==0)
filterWavelet = [-1 1 0; 1 0 -1; 0 -1 1]/sqrt(6);
elseif (fase==90)
filterWavelet = [-1 -1 2; -1 2 -1; 2 -1 -1]/sqrt(18);
end
elseif (orientasi==90)
if (fase==0)
filterWavelet = [-1 -1 -1; 0 0 0; 1 1 1]/sqrt(6);
elseif (fase==90)
filterWavelet = [-1 -1 -1; 2 2 2; -1 -1 -1]/sqrt(18);
end
elseif (orientasi==135)
if (fase==0)
filterWavelet = [0 -1 1; 1 0 -1; -1 1 0]/sqrt(6);
elseif (fase==90)
filterWavelet = [2 -1 -1; -1 2 -1; -1 -1 2]/sqrt(18);
end
end
if (isnan(filterWavelet))
disp('Parameter Wavelet tidak dikenali');
end
2b1c2. Lakukan proses filter menggunakan filter wavelet yang telah dihitung sebelumnya
Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah ini (poin 2b1c2a – 2b1c2c)
outputDekomposisi(y*ukuranSisi+1:y*ukuranSisi+ukuranSisi,x*ukuranSisi+1:x*ukuranSisi+ukuranSisi) = prosesFilter(img,filterWavelet);
2b1c2a. Hitung jumlah ukuran output filter pada level yang sedang terhitung
ukuranSisi = ukuran/3;
2b1c2b. Lakukan perkalian setiap elemen gambar dengan filter wavelet
imgFilter = img .* repmat(filterWavelet,ukuranSisi,ukuranSisi);
2b1c2c. Hasil proses filter adalah penjumlahan nilai pada setiap indeks kelipatan 3 dari indeks terpilih
outputFilter = zeros(ukuranSisi);
for y = 1:3
for x = 1:3
outputFilter = outputFilter + imgFilter(y:3:end,x:3:end);
end
end
2b2. Catat nilai dekomposisi tersebut ke dalam nilai output
ukuranDekomposisi = size(dekomposisiLevel,1); outputDekomposisi(end-ukuranDekomposisi+1:end,1:ukuranDekomposisi) = dekomposisiLevel/((3^level)^2);
2b3. Jika ukuran dekomposisi lebih dari satu,
maka perkecil ukuran gambar menjadi 1/3 ukuran semula untuk digunakan pada perhitungan level berikutnya
if (ukuranDekomposisi>1) ukuranDekomposisi = ukuranDekomposisi/3; img = dekomposisiLevel(end-ukuranDekomposisi+1:end,1:ukuranDekomposisi); end
3. Lakukan proses perhitungan dengan menggunakan metode Inversi BWT
Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah ini (poin 3a – 3b)
imgibwt = ibwt(imgbwt);
Memasuki proses pada fungsi IBWT
3a. Hitung jumlah level dekomposisi yang akan dilakukan, yaitu pangkat dari ukuran gambar
jumlahLevel = log(ukuran)/log(3);
3b. Lakukan perulangan sebanyak jumlah level (poin 3b1 – 3b4)
for level = 1:jumlahLevel . . .
3b1. Hitung ukuran sisi yang digunakan dalam perhitungan level ini
Kemudian simpan gambar input sebagai output dekomposisi sementara
Dan kosongkan semua nilai awal pada output yang akan dihitung
ukuranSisi = size(imgbwt,1); outputDekomposisi = imgbwt; if (ukuranSisi>3) outputDekomposisi(end-ukuranSisi/3+1:end,1:ukuranSisi/3) = 0; end
3b2. Lakukan proses dekomposisi gambar pada level yang sedang terpilih
Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah ini (poin 3b2a – 3b2c)
dekomposisiLevel = ibwtPerLevel(outputDekomposisi)/ukuran*ukuranSisi*((3^level)^2);
Memasuki perhitungan pada fungsi ibwtPerLevel
3b2a. Hitung jumlah ukuran output gambar pada level yang sedang terhitung
ukuranSisi = ukuran/3;
3b2b. Inisialisasi parameter orientasi untuk digunakan dalam proses filter
Orientasi yang digunakan adalah berukuran 3 x 3, dengan nilai sebagai berikut:
[ 90-odd 135-odd 45-even ]
[ 90-even 135-even 45-odd ]
[ DC 0-even 0 -odd ]
orientasi = [90 0; 135 0; 45 90; ...
90 90; 135 90; 45 0; ...
-1 -1; 0 90; 0 0];
3b2c. Lakukan perhitungan pada masing-masing orientasi tersebut (poin 3b2c1 – 3b2c2)
for i = 1:size(orientasi,1) . . .
3b2c1. Hitung filter wavelet pada orientasi tersebut
Penjelasan tentang fungsi ini sudah dijelaskan pada perhitungan sebelumnya
[~, idxMinimal] = min(jarakEuclidean);
3b2c2. Lakukan proses rekonstruksi gambar menggunakan filter wavelet yang telah dihitung sebelumnya
Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah ini (poin 3b2c2a – 3b2c2c)
img = img + rekonstruksiGambar(outputDekomposisi(y*ukuranSisi+1:y*ukuranSisi+ukuranSisi,x*ukuranSisi+1:x*ukuranSisi+ukuranSisi),filterWavelet);
Memasuki perhitungan pada fungsi rekonstruksiGambar
3b2c2a. Hitung jumlah ukuran output gambar pada level yang sedang terhitung
ukuran = ukuranGambar(1);
3b2c2b. Lakukan proses upsample koefisien dekomposisi dengan ukuran skala 3 kali ukuran semula
idx = ceil((1:3*ukuran)/3); koefisienDekomposisi = koefisienDekomposisi(idx,idx);
3b2c2c. Lakukan perkalian setiap elemen gambar dengan koefisien dekomposisi
img = koefisienDekomposisi .* repmat(filterWavelet,ukuran,ukuran);
3b3. Lakukan proses upsample dengan ukuran skala ukuran gambar / ukuran sisi
idx = ceil((1:ukuran)*ukuranSisi/ukuran); imgibwt = imgibwt + dekomposisiLevel(idx,idx);
3b4. Jika ukuran sisi lebih dari satu,
maka perkecil ukuran gambar menjadi 1/3 ukuran semula untuk digunakan pada perhitungan level berikutnya
if (ukuranSisi>1) imgbwt = imgbwt(end-ukuranSisi/3+1:end,1:ukuranSisi/3); end
* Tamplikan hasil akhir
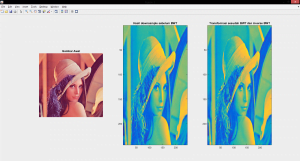
imagesc(imgibwt); title('Transformasi sesudah BWT dan inverse BWT');
Hasil akhir adalah: (klik untuk perbesar gambar)
Contoh modul / source code menggunakan Matlab dapat didownload disini:
[sdm_download id=”2758″ fancy=”0″]
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.

Leave a Reply