Algoritma GSA (Gravitational Search Algorithm) adalah salah satu algoritma optimasi yang dapat digunakan untuk pengambilan keputusan. Contoh yang dibahas kali ini adalah mengenai pencarian posisi dengan pengembalian nilai fungsi maksimal.
Algoritma ini terinspirasi dari sebuah teori hukum gravitasi yaitu teori Newton. Inti dari teori tersebut adalah “Setiap partikel yang ada di dunia akan saling menarik satu sama lain dengan kekuatan yang berbanding lurus dengan massa partikel dan berbanding terbalik dengan jarak antar partikel tersebut”. Sistem tarik menarik tersebut yang akan digunakan dalam melakukan pemecahan permasalahan optimasi pada kasus ini.
Diasumsikan ada sebaran titik 2 dimensi antara -2 sampai dengan 2
Fungsi yang diketahui adalah fungsi Himmelblau, dengan rumus f(x, y) = (x^2+y-11)^2 + (x+y^2-7)^2
Tentukan posisi dimana fungsi tersebut mengembalikan nilai maksimal
Fungsi Himmelblau adalah salah satu fungsi yang dapat digunakan untuk mengoptimasi suatu permasalahan. Fungsi ini memiliki sebuah nilai maksimum pada x = -0.270845, and y = -0.923039 dengan nilai fungsi sebesar f(x,y) = 181.617, dengan asumsi bahwa rentang minimal dan maksimal dari sebaran titik adalah -2 sampai dengan 2
Grafik fungsi Himmelblau yang normal, atau untuk sebaran titik tak terbatas adalah sebagai berikut.
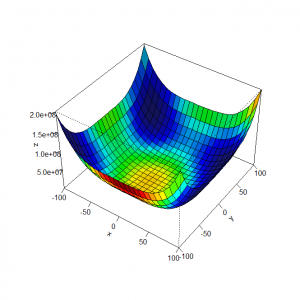
Sedangkan Grafik fungsi Himmelblau untuk sebaran titik dengan rentang minimal -2 dan maksimal 2 adalah sebagai berikut.
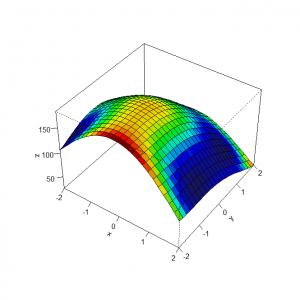
Dapat dilihat bahwa pada gambar tersebut, didapatkan area dengan titik tertinggi (berwarna merah) berada pada area x = -0, and y = -1, dimana titik tersebut mengembalikan nilai fungsi tertinggi. Oleh sebab itu digunakan algoritma ini untuk mencari titik di area berwarna merah tersebut.
Sebelum masuk kedalam langkah-langkah pembahasan algoritma, ada beberapa konstanta atau parameter yang harus diketahui, yaitu:
* Tentukan dimensi permasalahan dalam sebuah solusi
Diasumsikan dalam kasus ini, dimensi bernilai 2 karena ada 2 dimensi yang akan dicari solusinya yaitu x dan y
Const dimensi As Integer = 2
* Tentukan posisi minimal dan maksimal dari fungsi yang akan dihitung
Jika tidak ada batasan posisi, tentu saja posisi yang mendekati tak terhingga akan terpilih karena akan mengembalikan nilai fungsi yang sangat besar
Diasumsikan dalam kasus ini, posisi minimal adalah -2, dan posisi maksimal adalah +2
Const minPosisi As Double = -2 Const maksPosisi As Double = +2
* Tentukan jumlah iterasi yang digunakan dalam perhitungan
Diasumsikan dalam kasus ini, jumlah iterasi adalah 500 kali
Const jumlahIterasi As Integer = 500
* Tentukan jumlah individu yang digunakan
Diasumsikan dalam kasus ini, jumlah individu adalah 15 individu
Const jumlahIndividu As Integer = 15
* Tentukan persentase individu elit yang akan digunakan dalam proses perhitungan percepatan
Batas nilai yang digunakan adalah 1 sampai dengan jumlah individu
Diasumsikan dalam kasus ini, persentase individu elit adalah 2
Const persentaseIndividuElit As Integer = 2
Langkah-langkah penggunaan algoritma ini adalah
* Lakukan proses pencarian posisi terbaik
Penjelasan lebih detail tentang fungsi ini dapat dilihat pada penjelasan skrip dibawah ini (poin 1 – 2)
Dim posisiTerbaik() As Double = GSA(dimensi, minPosisi, maksPosisi, jumlahIterasi, jumlahIndividu, _ persentaseIndividuElit)
Memasuki perhitungan pada fungsi GSA
* Inisialisasi individu yang digunakan sebanyak parameter jumlah individu
1. Lakukan perulangan sebanyak jumlah individu (poin 1a – 1b)
For i As Integer = 0 To jumlahIndividu - 1 . . .
1a. Beri posisi acak pada masing-masing individu sebanyak jumlah dimensi
Kemudian hitung nilai fungsi pada posisi tersebut
Penjelasan lebih detail tentang fungsi ini dapat dilihat pada penjelasan skrip dibawah ini
For k As Integer = 0 To dimensi - 1 daftarIndividu(i).posisi(k) = (maksPosisi - minPosisi) * rnd.NextDouble() + minPosisi Next k daftarIndividu(i).nilaiFungsi = hitungNilaiFungsi(daftarIndividu(i).posisi)
* Gunakan fungsi ini untuk menghitung nilai fungsi yang diinginkan
Fungsi yang diketahui adalah fungsi Himmelblau, dengan rumus f(x, y) = (x^2+y-11)^2 + (x+y^2-7)^2
Public Function HitungNilaiFungsi(x1 As Double, y As Double) As Double Dim hasil As Double = Math.Pow(x1 * x1 + y - 11, 2) + Math.Pow(x1 + y * y - 7, 2) Return hasil End Function
1b. Ambil posisi individu terbaik sebagai posisi terbaik sementara
If daftarIndividu(i).nilaiFungsi > nilaiFungsiTerbaik Then Array.Copy(daftarIndividu(i).posisi, PosisiTerbaik, dimensi) nilaiFungsiTerbaik = daftarIndividu(i).nilaiFungsi End If
* Lakukan proses pencarian posisi terbaik (poin 2)
2. Lakukan proses perhitungan sebanyak jumlah iterasi (poin 2a – 2d)
Dim iterasi As Integer = 0 Do While iterasi < jumlahIterasi iterasi += 1 . . .
2a. Lakukan perhitungan untuk mencari konstanta gravitasi yang digunakan
Rumus yang digunakan bisa diganti sesuai kebutuhan, dengan catatan bahwa
Semakin lama perulangan yang dilakukan, maka nilai konstanta gravitasi akan semakin turun mendekati 0
Const alpha As Double = 20 Const g0 As Double = 1 Dim G As Double = g0 * Math.Exp(-alpha * iterasi / jumlahIterasi)
* Memasuki proses perhitungan massa dari masing-masing individu (poin 2b)
2b1. Tentukan nilai fungsi terendah dan tertinggi dari daftar individu
Dim nilaiFungsiTertinggi As Double = Double.MinValue Dim nilaiFungsiTerendah As Double = Double.MaxValue For i As Integer = 0 To jumlahIndividu - 1 If daftarIndividu(i).nilaiFungsi > nilaiFungsiTertinggi Then nilaiFungsiTertinggi = daftarIndividu(i).nilaiFungsi End If If daftarIndividu(i).nilaiFungsi < nilaiFungsiTerendah Then nilaiFungsiTerendah = daftarIndividu(i).nilaiFungsi End If Next
2b2. Hitung nilai massa dengan rumus:
m = (fit-min)/(maks-min)
Kemudian lakukan normalisasi dengan cara membagi massa dengan semua total massa yang ada
Dim totalMassa As Double = 0 For i As Integer = 0 To jumlahIndividu - 1 daftarIndividu(i).massa = (daftarIndividu(i).nilaiFungsi - nilaiFungsiTerendah) / (nilaiFungsiTertinggi - nilaiFungsiTerendah) totalMassa += daftarIndividu(i).massa Next For i As Integer = 0 To jumlahIndividu - 1 daftarIndividu(i).massa /= totalMassa Next
* Memasuki proses perhitungan percepatan di dalam ruang gravitasi (poin 2c)
2c1. Lakukan pengurutan pada daftar individu ini
Dim daftarIndividuTerurut() As Individu = daftarIndividu.Clone Array.Sort(daftarIndividuTerurut)
2c2. Tentukan jumlah individu terpilih yang digunakan dalam daftar individu terurut
Nantinya masing-masing individu akan mengalami pergerakan menuju individu-individu terbaik
Semakin lama perulangan, maka jumlah individu terpilih akan semakin sedikit untuk mengurangi pergerakan dari masing-masing individu
Dim jumlahIndividuElit As Integer = persentaseIndividuElit + (1 - iterasi / jumlahIterasi) * (100 - persentaseIndividuElit) jumlahIndividuElit = Math.Round(jumlahIndividu * jumlahIndividuElit / 100)
2c3. Lakukan perulangan pada masing-masing individu, dan bandingkan dengan individu terbaik sebanyak jumlah individu terpilih (poin 2c3a - 2c3b)
For i As Integer = 0 To jumlahIndividu - 1 For idxTerurut As Integer = 0 To jumlahIndividuElit - 1 . . .
2c3a. Hitung jarak Euclidean dari individu dan individu terpilih
Penjelasan tentang fungsi ini dapat dilihat pada penjelasan skrip dibawah ini
Dim jarakEuclidean As Double = hitungJarakEuclidean(daftarIndividu(i).posisi, daftarIndividuTerurut(idxTerurut).posisi, daftarIndividu(i).posisi.Length)
* Gunakan fungsi ini untuk menghitung jarak Euclidean antara 2 data
Private Function hitungJarakEuclidean(dataPertama As Double(), dataKedua As Double(), jumlahData As Integer) As Double
If dataPertama.Length <> dataKedua.Length Then
Throw New Exception("pada fungsi hitungJarakEuclidean, ukuran matriks data pertama tidak sama dengan ukuran matriks data kedua")
End If
Dim jumlah As Double = 0.0
For i As Integer = 0 To jumlahData - 1
Dim delta As Double = (dataPertama(i) - dataKedua(i)) * (dataPertama(i) - dataKedua(i))
jumlah += delta
Next
If jumlah > 0 Then
Return Math.Sqrt(jumlah)
Else
Return 0
End If
End Function
2c3b. Jika jarak Euclidean lebih dari 0,
maka hitung total jarak Euclidean dari masing-masing dimensi dengan rumus:
E = E + nilai acak * m(idxTerurut) * (X(idxTerurut) - X(i)) / (jarak + eps)
If jarakEuclidean > 0 Then For j As Integer = 0 To dimensi - 1 totalEuclidean(i)(j) += rnd.NextDouble * (daftarIndividuTerurut(idxTerurut).massa) * (daftarIndividuTerurut(idxTerurut).posisi(j) - daftarIndividu(i).posisi(j)) / (jarakEuclidean + 0.000001) Next End If
2c4. Hitung percepatan dengan cara perkalian total jarak Euclidean dengan konstanta gravitasi
Dim percepatan(jumlahIndividu - 1)() As Double
For i As Integer = 0 To jumlahIndividu - 1
percepatan(i) = New Double(dimensi - 1) {}
For j As Integer = 0 To dimensi - 1
percepatan(i)(j) = totalEuclidean(i)(j) * G
Next
Next
2d. Lakukan perhitungan pada masing-masing dimensi dalam individu (poin 2d1 - 2d4)
For i As Integer = 0 To jumlahIndividu - 1 For j As Integer = 0 To dimensi - 1 . . .
2d1. Hitung kecepatan pergerakan individu dengan rumus:
v baru = v lama * nilai acak + percepatan
Kemudian lakukan perpindahan posisi yang baru dengan cara menjumlahkan posisi lama dengan kecepatan pergerakan
kecepatan(i)(j) = kecepatan(i)(j) * rnd.NextDouble + percepatan(i)(j) daftarIndividu(i).posisi(j) += kecepatan(i)(j)
2d2. Jika posisi individu tersebut ternyata diluar batas posisi yang diperbolehkan,
maka kembalikan nilainya agar masuk dalam batas tersebut
If daftarIndividu(i).posisi(j) < minPosisi Then daftarIndividu(i).posisi(j) = minPosisi ElseIf daftarIndividu(i).posisi(j) > maksPosisi Then daftarIndividu(i).posisi(j) = maksPosisi End If
2d3. Hitung nilai fungsi pada individu tersebut
daftarIndividu(i).nilaiFungsi = hitungNilaiFungsi(daftarIndividu(i).posisi)
2d4. Jika nilai fungsi terbaik pada individu tersebut ternyata lebih baik dari nilai fungsi secara umum,
maka ambil posisi terbaik individu tersebut sebagai posisi terbaik
If daftarIndividu(i).nilaiFungsi > nilaiFungsiTerbaik Then
Array.Copy(daftarIndividu(i).posisi, PosisiTerbaik, dimensi)
nilaiFungsiTerbaik = daftarIndividu(i).nilaiFungsi
Console.Write("Iterasi " & iterasi.ToString.PadRight(4) & ", ")
Console.Write("individu " & i.ToString.PadRight(2) & ", ")
Console.Write("Posisi sementara: [")
For j As Integer = 0 To PosisiTerbaik.Length - 1
Console.Write(PosisiTerbaik(j).ToString("F4").PadLeft(7) & " ")
Next j
Console.Write("], ")
Console.WriteLine("nilai fungsi = " & nilaiFungsiTerbaik.ToString("F6"))
End If
* Agar dapat menjalankan skrip diatas, maka diperlukan sebuah Class Universe untuk menampung semua data posisi dan nilai fungsinya. Deklarasi Class Universe adalah sebagai berikut:
Public Class Individu
Implements IComparable(Of Individu)
Implements ICloneable
Public posisi() As Double
Public nilaiFungsi As Double
Public massa As Double
Public Sub New(ByVal dimensi As Integer)
Me.posisi = New Double(dimensi - 1) {}
Me.nilaiFungsi = 0.0
Me.massa = 0.0
End Sub
. . .
End Class
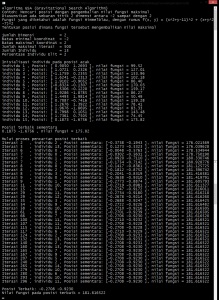
Hasil akhir adalah: (klik untuk perbesar gambar)
Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:
[sdm_download id="2818" fancy="0"]
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.

Leave a Reply