Algoritma ElGamal adalah salah satu algoritma yang dapat digunakan untuk melakukan enkripsi data sehingga data asli hanya dapat dibaca oleh seseorang yang memiliki kunci enkripsi tersebut. Contoh yang dibahas kali ini adalah mengenai enkripsi dan dekripsi dari sebuah kalimat.
Langkah-langkah penggunaan algoritma ini adalah
* Karena perhitungan menggunakan angka-angka yang sangat besar, maka diperlukan tipe BigInteger yang mampu memuat bilangan hingga tak terbatas
Untuk dapat menggunakan tipe data ini, maka harus dilakukan penambahan reference bernama System.Numerics pada saat pembuatan project
Kemudian melakukan import namespace System.Numerics
Imports System.Numerics
* Tentukan kalimat yang digunakan sebagai data input
Diasumsikan data input adalah sebagai berikut:
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.
1. Lakukan proses pembuatan kata kunci enkripsi (poin 1a – 1c)
1a. Tentukan bilangan prima secara acak
Penjelasan lebih detail tentang fungsi ini dapat dilihat pada penjelasan skrip dibawah ini
Dim bilanganPrima As Integer = getBilanganPrima(rnd, Byte.MaxValue, UShort.MaxValue) Dim p As New BigInteger(bilanganPrima)
* Gunakan fungsi ini untuk mendapatkan bilangan prima pada rentang tertentu
Bilangan prima adalah bilangan yang menghasilkan sisa pembagian 0 apabila dibagi dengan bilangan 1 dan dirinya sendiri
Public Function getBilanganPrima(ByVal rnd As Random, ByVal min As Integer, ByVal maks As Integer) As Integer Dim n As Integer = 0 Dim isBilanganPrima As Boolean = True Do isBilanganPrima = True n = rnd.Next(min, maks) Dim startCount As Integer = Math.Round(n / 2) If startCount Mod 2 = 0 Then startCount -= 1 End If For i As Integer = startCount To 3 Step -2 If n Mod i = 0 Then isBilanganPrima = False Exit For End If Next If n Mod 2 = 0 Then isBilanganPrima = False Loop Until isBilanganPrima = True Return n End Function
1b. Tentukan kata kunci acak yang berada diantara 1 sampai dengan bilangan prima – 1
Dim keyAcak As Integer = rnd.Next(1, p - 1) Dim key As New BigInteger(keyAcak)
1c. Tentukan g secara acak,
kemudian hitung h dengan rumus:
h = g ^ key mod p
Dim g As Integer = rnd.Next(Byte.MaxValue) Dim h As BigInteger = BigInteger.ModPow(g, key, p)
2. Lakukan enkripsi kalimat awal menggunakan algoritma ini
* Lakukan perhitungan pada masing-masing karakter dalam kalimat
Lakukan proses enkripsi untuk karakter ini.
Penjelasan lebih detail tentang fungsi ini dapat dilihat pada penjelasan skrip dibawah ini
For i As Integer = 0 To input.Length - 1
Dim data As Integer = AscW(input(i))
Dim m As New BigInteger(data)
cipher(i) = prosesEnkripsi(p, g, h, m, rnd)
Console.WriteLine("c1 = " & cipher(i)(0).ToString.PadLeft(5) & ", c2 = " & cipher(i)(1).ToString.PadLeft(5))
Next
* Gunakan fungsi ini untuk melakukan proses enkripsi
Dapatkan nilai y acak
Hitung c1 = g ^ y mod p
Hitung s = h ^ y mod p
Hitung c2 = m * s mod p
Public Function prosesEnkripsi(ByVal p As BigInteger, ByVal g As BigInteger, ByVal h As BigInteger, ByVal m As Integer, ByVal rnd As Random) As Integer()
Dim key As Integer = rnd.Next(Byte.MaxValue)
Dim y As BigInteger = New BigInteger(key)
Dim c1 As BigInteger = BigInteger.ModPow(g, y, p)
Dim s As BigInteger = BigInteger.ModPow(h, y, p)
Dim c2 As BigInteger = BigInteger.Multiply(m, s) Mod p
Return New Integer() {c1, c2}
End Function
3. Lakukan dekripsi dari kalimat yang telah terenkripsi
* Lakukan perhitungan pada masing-masing cipher yang telah ditemukan
Lakukan proses dekripsi dari cipher yang tersedia
Penjelasan lebih detail tentang fungsi ini dapat dilihat pada penjelasan skrip dibawah ini
For i As Integer = 0 To input.Length - 1 m1(i) = prosesDekripsi(cipher(i), p, key, rnd) Console.Write(ChrW(m1(i))) Next
* Gunakan fungsi ini untuk melakukan proses dekripsi
Hitung s2 = c1 * key mod p
Hitung m’ = c2 * invers modulus s
Public Function prosesDekripsi(ByVal cipher() As Integer, ByVal p As BigInteger, ByVal key As BigInteger, ByVal rnd As Random) As Integer Dim s2 As BigInteger = BigInteger.ModPow(cipher(0), key, p) Dim s2modInverse As BigInteger = modInverse(s2, p) Dim m As BigInteger = BigInteger.Multiply(cipher(1), s2modInverse) Mod p Return m End Function
* Gunakan fungsi ini untuk menghitung modular multiplicative inverse
hasil perhitungan adalah nilai x yang memenuhi syarat
n x = 1 (mod m)
Jika n = 3 dan m = 11,
maka x = 4, karena (4 * 3) mod 11 = 1
Sehingga dapat dikatakan 4 adalah invers modulus dari 3
Public Function modInverse(ByVal n As BigInteger, m As BigInteger) As BigInteger
n = n Mod m
For x As Integer = 0 To m - 1
If (n * x) Mod m = 1 Then Return x
Next
Return 0
End Function
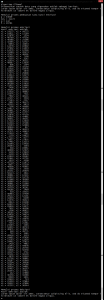
Hasil akhir adalah: (klik untuk perbesar gambar)
Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:
[sdm_download id=”3369″ fancy=”0″]
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.

Leave a Reply