Algoritma Kruskal adalah salah satu algoritma yang digunakan untuk pencarian jalur. Contoh yang dibahas kali ini adalah mengenai menghubungkan semua titik dengan biaya terendah.
Berbeda dengan algoritma pencarian jalur yang lain, seperti Algoritma Dijkstra dan Algoritma A* (A-Star) yang sudah pernah dibahas sebelumnya, algoritma ini hanya bertujuan untuk menghubungkan semua titik, bukan untuk mencari jalur yang tersambung dari awal sampai akhir. Contoh kasus nyata yang dapat digunakan adalah menghubungkan semua komputer dalam 1 jaringan pada sebuah warnet. Jika terdapat pemasangan komputer baru, tentu saja cukup dihubungkan dengan komputer terdekat, tidak perlu langsung dihubungkan dengan komputer induk, kecuali jika komputer induk memang merupakan komputer terdekat.
Diasumsikan ada 5 titik yang harus dihubungkan semuanya, yaitu titik A,B,C,D,E
semua titik tidak terhubung secara langsung dengan titik-titik lainnya, melainkan hanya melalui jalur tertentu saja
setiap jalur juga memiliki biaya sendiri-sendiri
Tentukan jalur yang harus diambil untuk menghubungkan semua titik dengan biaya terendah
Diasumsikan data jalur yang tersedia adalah sebagai berikut
| Titik awal | Titik Tujuan | Biaya |
|---|---|---|
| Titik A | Titik B | 6 |
| Titik A | Titik E | 7 |
| Titik B | Titik C | 5 |
| Titik B | Titik D | 4 |
| Titik B | Titik E | 8 |
| Titik C | Titik D | 7 |
| Titik C | Titik E | 3 |
| Titik D | Titik E | 9 |
Jika diilustrasikan dalam gambar, maka model data awal adalah sebagai berikut
Sebelum masuk kedalam langkah-langkah pembahasan algoritma, ada beberapa konstanta atau parameter yang harus diketahui, yaitu:
* Tentukan jumlah titik yang harus dihubungkan
Diasumsikan dalam kasus ini, jumlah titik ada 5 buah
Const jumlahTitik As Integer = 5
Langkah-langkah penggunaan algoritma ini adalah
1. Inisialisasi semua variabel yang diperlukan, yaitu variabel gambar, titik, garis, dan subset
Penjelasan tentang masing-masing class akan dijelaskan pada skrip dibawah ini
Console.WriteLine("Masukkan kata yang akan dicari usulannya: ")
Dim gmb As New Gambar(jumlahTitik)
Dim daftarTitik As Titik() = gmb.daftarTitik
Dim daftarGaris As New List(Of Garis)()
Dim grs As Garis
Dim daftarSubset As Subset() = New Subset(jumlahTitik - 1) {}
For i As Integer = 0 To jumlahTitik - 1
daftarSubset(i) = New Subset(daftarTitik(i), 0)
Next
Dim hasil As Garis() = New Garis(jumlahTitik - 1) {}
* Agar dapat menjalankan skrip diatas, maka diperlukan sebuah 4 buah class
Class Titik digunakan untuk menampung data titik
Class Garis digunakan untuk menampung data titik awal, titik tujuan, dan biaya jalur tersebut
Class Subset digunakan untuk menampung data induk dan peringkat pada masing-masing titik
Class Gambar digunakan untuk menampung semua data titik dan semua data garis yang digunakan
Deklarasi masing-masing class adalah sebagai berikut:
Public Class Gambar
Public daftarGaris As List(Of Garis) = Nothing
Public daftarTitik As Titik() = Nothing
Public Sub New(jumlahTitik As Integer)
daftarTitik = New Titik(jumlahTitik - 1) {}
For i As Integer = 0 To jumlahTitik - 1
daftarTitik(i) = New Titik(Chr(i + 65))
Next
End Sub
End Class
Public Class Subset
Private m_induk As Titik
Private m_peringkat As Integer
Public Property induk() As Titik
Get
Return m_induk
End Get
Set(value As Titik)
m_induk = value
End Set
End Property
Public Property peringkat() As Integer
Get
Return m_peringkat
End Get
Set(value As Integer)
m_peringkat = value
End Set
End Property
Public Sub New(ByVal induk As Titik, ByVal peringkat As Integer)
m_induk = induk
m_peringkat = peringkat
End Sub
End Class
Public Class Garis
Private m_titikAwal As Titik
Private m_titikTujuan As Titik
Private m_biaya As Integer
Public Property titikAwal() As Titik
Get
Return m_titikAwal
End Get
Set(value As Titik)
m_titikAwal = value
End Set
End Property
Public Property titikTujuan() As Titik
Get
Return m_titikTujuan
End Get
Set(value As Titik)
m_titikTujuan = value
End Set
End Property
Public Property biaya() As Integer
Get
Return m_biaya
End Get
Set(value As Integer)
m_biaya = value
End Set
End Property
Public Sub New(titikAwal As Titik, titikTujuan As Titik, biaya As Integer)
m_titikAwal = titikAwal
m_titikTujuan = titikTujuan
m_biaya = biaya
End Sub
End Class
Public Class Titik
Private m_Label As String
Public Property Label() As String
Get
Return m_Label
End Get
Set(value As String)
m_Label = value
End Set
End Property
Public Sub New(ByVal label As String)
m_Label = label
End Sub
End Class
2. Masukkan data titik dan garis kedalam masing-masing variabel yang tersedia
grs = New Garis(daftarTitik(0), daftarTitik(1), 6) daftarGaris.Add(grs) grs = New Garis(daftarTitik(0), daftarTitik(4), 7) daftarGaris.Add(grs) grs = New Garis(daftarTitik(1), daftarTitik(2), 5) daftarGaris.Add(grs) grs = New Garis(daftarTitik(1), daftarTitik(3), 4) daftarGaris.Add(grs) grs = New Garis(daftarTitik(1), daftarTitik(4), 8) daftarGaris.Add(grs) grs = New Garis(daftarTitik(2), daftarTitik(3), 7) daftarGaris.Add(grs) grs = New Garis(daftarTitik(2), daftarTitik(4), 3) daftarGaris.Add(grs) grs = New Garis(daftarTitik(3), daftarTitik(4), 9) daftarGaris.Add(grs) gmb.daftarGaris = daftarGaris.ToList().OrderBy(Function(p) p.biaya).ToList()
3. Lakukan proses pencarian garis sebanyak jumlah garis (poin 3a – 3c)
3a. Tentukan garis yang akan dicari apakah garis tersebut jalur terbaik atau bukan
grs = gmb.daftarGaris.ElementAt(idxGaris)
3b. Cari induk dari titik awal dan induk dari titik tujuan dari garis tersebut
Penjelasan tentang fungsi ini akan dijelaskan pada perhitungan dibawah ini
Dim titikAwal As Titik = cariIndukTitik(daftarSubset, grs.titikAwal, Array.IndexOf(gmb.daftarTitik, grs.titikAwal), gmb.daftarTitik) Dim titikTujuan As Titik = cariIndukTitik(daftarSubset, grs.titikTujuan, Array.IndexOf(gmb.daftarTitik, grs.titikTujuan), gmb.daftarTitik)
3c. Jika induk dari titik awal tidak sama dengan induk dari titik tujuan, maka lakukan perhitungan berikut:
3c1. Lakukan penggabungan kedua titik tersebut dalam sebuah subset
Jika peringkat titik pertama kurang dari peringkat titik kedua, maka jadikan titik kedua sebagai induk dari titik pertama
Jika peringkat titik pertama lebih dari peringkat titik kedua, maka jadikan titik pertama sebagai induk dari titik kedua
Jika peringkat kedua titik sama, maka jadikan titik pertama sebagai induk dari titik kedua dan tambahkan peringkat titik pertama dengan 1
If daftarSubset(Array.IndexOf(gmb.daftarTitik, titikAwal)).peringkat < daftarSubset(Array.IndexOf(gmb.daftarTitik, titikTujuan)).peringkat Then daftarSubset(Array.IndexOf(gmb.daftarTitik, titikAwal)).induk = titikTujuan ElseIf daftarSubset(Array.IndexOf(gmb.daftarTitik, titikAwal)).peringkat > daftarSubset(Array.IndexOf(gmb.daftarTitik, titikTujuan)).peringkat Then daftarSubset(Array.IndexOf(gmb.daftarTitik, titikTujuan)).induk = titikAwal Else daftarSubset(Array.IndexOf(gmb.daftarTitik, titikTujuan)).induk = titikAwal daftarSubset(Array.IndexOf(gmb.daftarTitik, titikAwal)).peringkat += 1 End If
3c2. Masukan garis terpilih sebagai salah satu garis jawaban
hasil(iterasi) = grs
4. Catat hasil akhir untuk masing-masing jawaban garis yang ditemukan
Kemudian jumlahkan total biaya garis tersebut
Dim jumlahBiaya As Integer = 0
For i As Integer = 0 To iterasi - 1
Console.WriteLine("Jalur " & i + 1 & " adalah dari titik " & hasil(i).titikAwal.Label & " ke titik " & hasil(i).titikTujuan.Label & " dengan biaya " & hasil(i).biaya)
jumlahBiaya += hasil(i).biaya
Next
Console.WriteLine("Total biaya = " & jumlahBiaya)
Hasil akhir adalah: (klik untuk perbesar gambar)
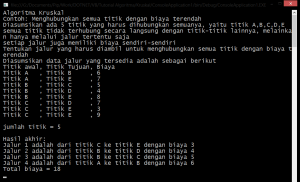
Jika diilustrasikan dalam gambar, maka model hasil akhirnya adalah sebagai berikut
Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:
[sdm_download id=”1336″ fancy=”0″]
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.
