Permasalahan Knapsack salah satu permasalahan optimasi. Bagaimana caranya seseorang dapat membawa sejumlah barang yang tidak melebihi kapasitas, tetapi dengan nilai barang yang paling tinggi.
Contoh kasus adalah sebagai berikut. Ada seseorang yang ingin berwisata ke gunung, sedangkan dia hanya dapat membawa sebuah ransel yang isinya terbatas. Diantara barang-barang yang perlu dibawa seperti baju, celana, handuk, jaket, kamera, kaos kaki, kompas, peta, sarung tangan, senter; masing-masing memiliki berat dan nilai prioritas. Sehingga barang-barang mana saja yang harus dibawa masuk ke dalam ransel dengan berat yang tidak melewati kapasitas ransel tetapi dengan nilai barang yang paling tinggi.
ada tiga variasi dasar dari permasalahan knapsack, yaitu
- UKP (Unbounded Knapsack Problem)
Dalam variasi ini, semua benda diasumsikan memiliki jumlah tidak terbatas, sehingga sebuah barang dapat dimasukkan ke dalam ransel dengan jumlah berapapun selama masih memenuhi batas kapasitas ransel
- 0/1 (0/1 Knapsack Problem)
Dalam variasi ini, semua benda diasumsikan memiliki jumlah 1, sehingga perhitungan yang dilakukan akan menentukan sebuah barang masuk / tidak masuk ke dalam ransel
- BKP (Bounded Knapsack Problem)
Dalam variasi ini, semua benda diasumsikan memiliki batas jumlah sendiri-sendiri, sehingga sebuah barang yang masuk ke dalam ransel harus memenuhi batas jumlah tersebut
Dalam kehidupan nyata, kasus BKP (Bounded Knapsack Problem) adalah kasus yang paling nyata, sehingga paling banyak digunakan dalam bidang lain. Pada contoh kasus ini akan dibahas semua variasi dasar tersebut untuk mengetahui perbedaan perhitungan antara ketiga variasi dasar tersebut.
Perlu diketahui, untuk masing-masing variasi dasar dapat diselesaikan oleh beberapa cara, yaitu
- Greedy Algorithm
- Dynamic Programming
- Dominance Relations
Sedangkan Greedy Algorithm sendiri memiliki 3 teknik perhitungan, yaitu
- Berat Terendah
Prioritas barang yang dihitung terlebih dahulu adalah dengan berat terendah, sehingga lebih banyak barang akan dapat masuk ke dalam ransel
- Nilai Tertinggi
Prioritas barang yang dihitung terlebih dahulu adalah dengan nilai tertinggi, sehingga barang-barang dengan nilai tertinggi akan masuk ke dalam ransel
- Rasio Nilai/Berat
Nilai barang akan dinormalisasi dengan cara dibagi berat barang tersebut. Prioritas barang yang dihitung terlebih dahulu adalah dengan nilai rasio tertinggi, yaitu barang-barang yang cukup bernilai tinggi dengan berat yang cukup rendah
Pada contoh kasus ini tidak semuanya akan dihitung, tetapi hanya akan diambil teknik yang berbeda saja untuk menunjukkan cara teknik perhitungan yang dimaksud.
Diasumsikan ada 10 buku yang dapat dibawa ke dalam sebuah knapsack, yaitu buku A,B,C,D,E,F,G,H,I,J
masing-masing buku memiliki berat dan nilai sendiri-sendiri
Maka tentukan buku apa saja yang seharusnya dibawa dengan berat yang tidak melebihi kapasitas dan dengan nilai tertinggi
UKP (Unbounded Knapsack Problem)
Teknik yang digunakan adalah Greedy Algorithm dengan prioritas berdasarkan berat terendah
Semua buku tersebut diasumsikan tidak terbatas jumlahnya
Diasumsikan data buku yang tersedia adalah sebagai berikut
| Nama Barang | Berat | Nilai | Jumlah |
|---|---|---|---|
| Buku A | 25 | 30 | Tidak Terbatas |
| Buku B | 27 | 20 | Tidak Terbatas |
| Buku C | 19 | 15 | Tidak Terbatas |
| Buku D | 33 | 35 | Tidak Terbatas |
| Buku E | 27 | 25 | Tidak Terbatas |
| Buku F | 29 | 40 | Tidak Terbatas |
| Buku G | 32 | 30 | Tidak Terbatas |
| Buku H | 38 | 50 | Tidak Terbatas |
| Buku I | 37 | 40 | Tidak Terbatas |
| Buku J | 21 | 20 | Tidak Terbatas |
Contoh data buku tersebut adalah sebagai berikut:
Dim unboundedItems = New List(Of UnboundedBarang)() From { _
New UnboundedBarang("Buku A", 25, 30, Integer.MaxValue), _
New UnboundedBarang("Buku B", 27, 20, Integer.MaxValue), _
New UnboundedBarang("Buku C", 19, 25, Integer.MaxValue), _
New UnboundedBarang("Buku D", 33, 35, Integer.MaxValue), _
New UnboundedBarang("Buku E", 27, 25, Integer.MaxValue), _
New UnboundedBarang("Buku F", 29, 40, Integer.MaxValue), _
New UnboundedBarang("Buku G", 32, 30, Integer.MaxValue), _
New UnboundedBarang("Buku H", 38, 50, Integer.MaxValue), _
New UnboundedBarang("Buku I", 37, 40, Integer.MaxValue), _
New UnboundedBarang("Buku J", 21, 20, Integer.MaxValue) _
}
* Agar dapat menjalankan skrip diatas, maka diperlukan sebuah Class UnboundedBarang untuk menampung semua data barang seperti nama, berat, nilai, dan batas jumlah sebuah barang. Deklarasi Class UnboundedBarang adalah sebagai berikut:
Public Class UnboundedBarang
Implements IComparable(Of UnboundedBarang)
Public namaBarang As String
Public berat As Integer
Public nilai As Integer
Public jumlahBarang As Integer
Public Sub New(namaBarang As String, berat As Integer, nilai As Integer, jumlahBarang As Integer)
Me.namaBarang = namaBarang
Me.berat = berat
Me.nilai = nilai
Me.jumlahBarang = jumlahBarang
End Sub
'Fungsi untuk mengurutkan berat dari yang terendah (terbaik) ke tertinggi (terburuk)
Public Function CompareTo(ByVal BarangLain As UnboundedBarang) As Integer Implements IComparable(Of UnboundedBarang).CompareTo
If Me.berat < BarangLain.berat Then
Return -1
ElseIf Me.berat > BarangLain.berat Then
Return 1
Else
Return 0
End If
End Function
End Class
Sebelum masuk kedalam langkah-langkah pembahasan algoritma, ada beberapa konstanta atau parameter yang harus diketahui, yaitu:
* Tentukan kapasitas knapsack yang ada
Diasumsikan dalam kasus ini, kapasitas knapsack adalah 100 satuan
Const unboundedKapasitas As Integer = 100
Langkah-langkah penggunaan algoritma ini adalah
1. Lakukan pengurutan barang dari berat terendah ke berat tertinggi
Skrip pengurutan sudah terdapat dalam skrip Class unboundedBarang diatas
unboundedBarangs.Sort()
2. Lakukan perulangan pada semua barang (poin 2a – 2c)
2a. Tentukan jumlah Barang, yaitu = sisa kapasitas / berat barang
Dim jumlahBarang As Integer = Math.Truncate((unboundedKapasitas - unboundedtotalBerat) / unboundedBarangs(i).berat)
2b. Catat total berat, yaitu berat barang * jumlah Barang
Dim tmpberat As Integer = unboundedBarangs(i).berat * jumlahBarang
2c. Apabila total berat masih kurang dari kapasitas,
maka masukkan Barang ini sejumlah jumlah Barang ke dalam hasil jawaban
Kemudian catat total berat dan total nilai yang sudah dikumpulkan
If unboundedtotalBerat + tmpberat <= unboundedKapasitas Then unboundedHasil.Add(unboundedBarangs(i)) unboundedHasil(unboundedHasil.Count - 1).jumlahBarang = jumlahBarang unboundedtotalBerat += tmpberat unboundedtotalNilai += unboundedBarangs(i).nilai * jumlahBarang End If
3. Tampilkan hasil perhitungan akhir pada layar
Console.WriteLine("Hasil Perhitungan: ")
Console.WriteLine("Total Berat: " & unboundedtotalBerat)
Console.WriteLine("Total Nilai: " & unboundedtotalNilai)
Console.WriteLine()
Console.WriteLine("Isi Knapsack:")
For i As Integer = 0 To unboundedHasil.Count - 1
Console.WriteLine(unboundedHasil(i).namaBarang & " (" & unboundedHasil(i).jumlahBarang & " buah)")
Next
0/1 (0/1 Knapsack Problem)
Teknik yang digunakan adalah Greedy Algorithm dengan prioritas berdasarkan nilai tertinggi
Semua buku tersebut diasumsikan hanya memiliki jumlah 1 buah
Diasumsikan data buku yang tersedia adalah sebagai berikut
| Nama Barang | Berat | Nilai | Jumlah |
|---|---|---|---|
| Buku A | 25 | 30 | 1 |
| Buku B | 27 | 20 | 1 |
| Buku C | 19 | 15 | 1 |
| Buku D | 33 | 35 | 1 |
| Buku E | 27 | 25 | 1 |
| Buku F | 29 | 40 | 1 |
| Buku G | 32 | 30 | 1 |
| Buku H | 38 | 50 | 1 |
| Buku I | 37 | 40 | 1 |
| Buku J | 21 | 20 | 1 |
Contoh data buku tersebut adalah sebagai berikut:
Dim nolSatuBarangs = New List(Of NolSatuBarang)() From { _
New NolSatuBarang("Buku A", 25, 30, 1), _
New NolSatuBarang("Buku B", 27, 20, 1), _
New NolSatuBarang("Buku C", 19, 25, 1), _
New NolSatuBarang("Buku D", 33, 35, 1), _
New NolSatuBarang("Buku E", 27, 25, 1), _
New NolSatuBarang("Buku F", 29, 40, 1), _
New NolSatuBarang("Buku G", 32, 30, 1), _
New NolSatuBarang("Buku H", 38, 50, 1), _
New NolSatuBarang("Buku I", 37, 40, 1), _
New NolSatuBarang("Buku J", 21, 20, 1) _
}
* Agar dapat menjalankan skrip diatas, maka diperlukan sebuah Class nolSatuBarang untuk menampung semua data barang seperti nama, berat, nilai, dan batas jumlah sebuah barang. Deklarasi Class nolSatuBarang adalah sebagai berikut:
Public Class NolSatuBarang
Implements IComparable(Of NolSatuBarang)
Public namaBarang As String
Public berat As Integer
Public nilai As Integer
Public jumlahBarang As Integer
Public Sub New(namaBarang As String, berat As Integer, nilai As Integer, jumlahBarang As Integer)
Me.namaBarang = namaBarang
Me.berat = berat
Me.nilai = nilai
Me.jumlahBarang = jumlahBarang
End Sub
'Fungsi untuk mengurutkan harga dari yang tertinggi (terbaik) ke terendah (terburuk)
Public Function CompareTo(ByVal BarangLain As NolSatuBarang) As Integer Implements IComparable(Of NolSatuBarang).CompareTo
If Me.nilai > BarangLain.nilai Then
Return -1
ElseIf Me.nilai < BarangLain.nilai Then
Return 1
Else
Return 0
End If
End Function
End Class
Sebelum masuk kedalam langkah-langkah pembahasan algoritma, ada beberapa konstanta atau parameter yang harus diketahui, yaitu:
* Tentukan kapasitas knapsack yang ada
Diasumsikan dalam kasus ini, kapasitas knapsack adalah 100 satuan
Const nolSatuKapasitas As Integer = 100
Langkah-langkah penggunaan algoritma ini adalah
1. Lakukan pengurutan barang dari nilai tertinggi ke nilai terendah
Skrip pengurutan sudah terdapat dalam skrip Class nolSatuBarang diatas
nolSatuBarangs.Sort()
2. Lakukan perulangan pada semua barang (poin 2a – 2c)
2a. Tentukan jumlah Barang, yaitu = 1
Dim jumlahBarang As Integer = 1
2b. Catat total berat, yaitu berat barang * jumlah Barang
Dim tmpberat As Integer = nolSatuBarangs(i).berat * jumlahBarang
2c. Apabila total berat masih kurang dari kapasitas,
maka masukkan Barang ini sejumlah jumlah Barang ke dalam hasil jawaban
Kemudian catat total berat dan total nilai yang sudah dikumpulkan
If nolSatutotalBerat + tmpberat <= nolSatuKapasitas Then nolSatuHasil.Add(nolSatuBarangs(i)) nolSatuHasil(nolSatuHasil.Count - 1).jumlahBarang = jumlahBarang nolSatutotalBerat += tmpberat nolSatutotalNilai += nolSatuBarangs(i).nilai * jumlahBarang End If
3. Tampilkan hasil perhitungan akhir pada layar
Console.WriteLine("Hasil Perhitungan: ")
Console.WriteLine("Total Berat: " & nolSatutotalBerat)
Console.WriteLine("Total Nilai: " & nolSatutotalNilai)
Console.WriteLine()
Console.WriteLine("Isi Knapsack:")
For i As Integer = 0 To nolSatuHasil.Count - 1
Console.WriteLine(nolSatuHasil(i).namaBarang & " (" & nolSatuHasil(i).jumlahBarang & " buah)")
Next
BKP (Bounded Knapsack Problem)
Teknik yang digunakan adalah Dynamic Programing
Semua buku tersebut diasumsikan memiliki batas jumlah sendiri-sendiri
Diasumsikan data buku yang tersedia adalah sebagai berikut
| Nama Barang | Berat | Nilai | Jumlah |
|---|---|---|---|
| Buku A | 25 | 30 | 1 |
| Buku B | 27 | 20 | 2 |
| Buku C | 19 | 15 | 4 |
| Buku D | 33 | 35 | 3 |
| Buku E | 27 | 25 | 3 |
| Buku F | 29 | 40 | 2 |
| Buku G | 32 | 30 | 4 |
| Buku H | 38 | 50 | 1 |
| Buku I | 37 | 40 | 1 |
| Buku J | 21 | 20 | 2 |
Contoh data buku tersebut adalah sebagai berikut:
Dim boundedBarangs = New List(Of BoundedBarang)() From { _
New BoundedBarang("Buku A", 25, 30, 1), _
New BoundedBarang("Buku B", 27, 20, 2), _
New BoundedBarang("Buku C", 19, 25, 4), _
New BoundedBarang("Buku D", 33, 35, 3), _
New BoundedBarang("Buku E", 27, 25, 3), _
New BoundedBarang("Buku F", 29, 40, 2), _
New BoundedBarang("Buku G", 32, 30, 4), _
New BoundedBarang("Buku H", 38, 50, 1), _
New BoundedBarang("Buku I", 37, 40, 1), _
New BoundedBarang("Buku J", 21, 20, 2) _
}
* Agar dapat menjalankan skrip diatas, maka diperlukan 2 Class yaitu Class BoundedBarang untuk menampung semua data barang seperti nama, berat, nilai, dan batas jumlah sebuah barang, dan Class daftarBoundedBarang untuk menampung semua jawaban barang beserta total berat dan total nilai. Deklarasi Class BoundedBarang dan Class daftarBoundedBarang adalah sebagai berikut:
Public Class BoundedBarang
Public namaBarang As String
Public berat As Integer
Public nilai As Integer
Public jumlahBarang As Integer
Public Sub New(namaBarang As String, berat As Integer, nilai As Integer, jumlahBarang As Integer)
Me.namaBarang = namaBarang
Me.berat = berat
Me.nilai = nilai
Me.jumlahBarang = jumlahBarang
End Sub
End Class
Public Class daftarBoundedBarang
Public Isi As New Dictionary(Of String, Integer)()
Public totalNilai As Integer
Public totalBerat As Integer
Public Sub TambahBarang(Barang As BoundedBarang, jumlahBarang As Integer)
If Isi.ContainsKey(Barang.namaBarang) Then
Isi(Barang.namaBarang) += jumlahBarang
Else
Isi(Barang.namaBarang) = jumlahBarang
End If
totalNilai += jumlahBarang * Barang.nilai
totalBerat += jumlahBarang * Barang.berat
End Sub
Public Function salinDaftar() As daftarBoundedBarang
Dim ic = New daftarBoundedBarang()
ic.Isi = New Dictionary(Of String, Integer)(Me.Isi)
ic.totalNilai = Me.totalNilai
ic.totalBerat = Me.totalBerat
Return ic
End Function
End Class
Sebelum masuk kedalam langkah-langkah pembahasan algoritma, ada beberapa konstanta atau parameter yang harus diketahui, yaitu:
* Tentukan kapasitas knapsack yang ada
Diasumsikan dalam kasus ini, kapasitas knapsack adalah 100 satuan
Const boundedKapasitas As Integer = 100
Langkah-langkah penggunaan algoritma ini adalah
1. Lakukan perulangan untuk setiap kapasitas (j) pada semua barang (i)
Jika kapasitas ke j lebih dari berat barang ke i, maka lakukan perhitungan berikutnya
For i As Integer = 0 To boundedBarangs.Count - 1 For j As Integer = boundedKapasitas To 0 Step -1 If j >= boundedBarangs(i).berat Then . . .
2. Tentukan jumlah Barang, yaitu = nilai minimal antara batas minimal setiap barang atau nilai kapasitas ke j / berat barang
Dim jumlahBarang As Integer = Math.Min(boundedBarangs(i).jumlahBarang, Math.Truncate(j / boundedBarangs(i).berat))
3. Lakukan perulangan pada setiap jumlah Barang yang ditemukan (poin 3a – 3c)
3a. Catat barang pada kapasitas ke j – (jumlah Barang * berat barang)
Dim tmpDaftarBoundedBarang As daftarBoundedBarang = daftarBoundedBarangs(j - k * boundedBarangs(i).berat)
3b. Catat akumulasi nilai, yaitu total nilai + (jumlah Barang * nilai barang)
Dim tmpnilai As Integer = tmpDaftarBoundedBarang.totalNilai + k * boundedBarangs(i).nilai
3c. Apabila akumulasi nilai masih lebih dari total nilai,
maka masukkan Barang ini sejumlah jumlah Barang ke dalam hasil jawaban
If tmpnilai > daftarBoundedBarangs(j).totalNilai Then daftarBoundedBarangs(j) = tmpDaftarBoundedBarang.salinDaftar() daftarBoundedBarangs(j).TambahBarang(boundedBarangs(i), k) End If
4. Tampilkan hasil perhitungan akhir pada layar
Console.WriteLine("Hasil Perhitungan: ")
Console.WriteLine("Total Berat: " & daftarBoundedBarangs(boundedKapasitas).totalBerat)
Console.WriteLine("Total Nilai: " & daftarBoundedBarangs(boundedKapasitas).totalNilai)
Console.WriteLine()
Console.WriteLine("Isi Knapsack:")
For Each kvp As KeyValuePair(Of String, Integer) In daftarBoundedBarangs(boundedKapasitas).Isi
Console.WriteLine(kvp.Key & " (" & kvp.Value & " buah)")
Next
Hasil akhir untuk ketiga variasi permasalahan diatas adalah: (klik untuk perbesar gambar)
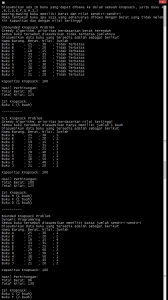
Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:
[sdm_download id=”1371″ fancy=”0″]
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.

Boleh tau referensi dalam menulis postingan ini? Saya membutuhkan buku untuk mengetahui ttg rasio diatas untuk skripsi saya. Terimakasih
Saya hanya menggunakan referensi wikipedia yang dapat anda akses melalui halaman https://en.wikipedia.org/wiki/Knapsack_problem
Dalam halaman tersebut pada bagian Dominance Relation dan sub bagian Modular Dominance terdapat kalimat yang intinya barang terbaik ditentukan dengan menggunakan rumus (vb / wb). Dengan kata lain (value b / weight b), atau diterjemahkan menjadi (nilai b / berat b). Inilah dasar nilai rasio yang saya gunakan dalam perhitungan diatas.
Pak, ada perhitungan manualnya tidak? Saya kurang bisa memahaminya karena saya tidak menguasai vb.
Saya tidak memiliki cara perhitungan manual untuk algoritma ini, tetapi konsep dari permasalahan knapsack cukup mudah sehingga perhitungannya dapat disusun secara manual setelah memahami konsep dari permasalahan tersebut.