Dalam statistika, regresi linear adalah sebuah pendekatan untuk memodelkan hubungan antara variable terikat Y dan satu atau lebih variable bebas yang disebut X. Salah satu kegunaan dari regresi linear adalah untuk melakukan prediksi berdasarkan data-data yang telah dimiliki sebelumnya. Contoh yang dibahas kali ini adalah menentukan hasil jual tipe sepeda motor baru berdasarkan kelompok data yang sudah ada.
Analisis regresi adalah salah satu analisis yang paling populer dan luas pemakaiannya. Analisis regresi dipakai secara luas untuk melakukan prediksi dan ramalan, dengan penggunaan yang saling melengkapi pada teknik pembelajaran.
Diasumsikan ada 4 tipe motor yang sudah diketahui datanya, yaitu Motor A,B,C,D
Masing-masing tipe motor memiliki kriteria, yaitu harga, jarak tempuh per liter, cc, dan memiliki hasil jual dalam unit
Diasumsikan data dari 4 tipe motor tersebut adalah sebagai berikut:
| Motor | Harga | Jarak tempuh per liter | cc | Unit Terjual |
|---|---|---|---|---|
| Motor A | 10.000.000 | 35 | 110 | 20 |
| Motor B | 12.000.000 | 45 | 125 | 9 |
| Motor C | 11.000.000 | 40 | 150 | 17 |
| Motor D | 14.000.000 | 37.5 | 125 | 12 |
Contoh data awal adalah sebagai berikut:
Dim data(3)() As Double
data(0) = New Double() {10000000, 35, 110, 20}
data(1) = New Double() {12000000, 45, 125, 9}
data(2) = New Double() {11000000, 40, 150, 17}
data(3) = New Double() {14000000, 37.5, 125, 12}
Selanjutnya ada 4 buah motor lagi, yaitu E,F,G,H, yang baru akan diluncurkan, sehingga tidak diketahui hasil jualnya
Maka tentukan data-data ini nantinya diperkirakan memiliki hasil jual berapa unit
Diasumsikan data awalnya adalah sebagai berikut:
| Motor | Harga | Jarak tempuh per liter | cc |
|---|---|---|---|
| Motor E | 13.000.000 | 45 | 125 |
| Motor F | 12.000.000 | 47 | 110 |
| Motor G | 10.500.000 | 43 | 110 |
| Motor H | 13.500.000 | 35 | 125 |
Contoh data baru yang akan dihitung adalah sebagai berikut:
Untuk kriteria Nilai Hasil:
Karena belum diketahui nilai hasilnya, maka semua inputan data adalah -1
Dim dataBaru(3)() As Double
dataBaru(0) = New Double() {13000000, 45, 125, -1}
dataBaru(1) = New Double() {12000000, 47, 110, -1}
dataBaru(2) = New Double() {10500000, 43, 110, -1}
dataBaru(3) = New Double() {13500000, 35, 125, -1}
Langkah-langkah penggunaan algoritma ini adalah
1. Tentukan matriks desain
Matriks desain adalah matriks data dengan penambahan kolom pertama yang bernilai 1 pada setiap barisnya
Penambahan kolom ini disebut kolom dummy, digunakan untuk menghitung koefisien beta 0 / intercept
Dim contohData(data.Length - 1)() As Double
For i As Integer = 0 To data.Length - 1
contohData(i) = New Double(data(i).Length) {}
contohData(i)(0) = 1
For j As Integer = 0 To data(i).Length - 1
contohData(i)(j + 1) = data(i)(j)
Next
Next
2. Hitung koefisien Beta untuk masing-masing kolom kriteria
koefisien beta yang dihitung adalah sejumlah kriteria + 1
koefisien beta pada indeks ke 0 adalah konstanta atau disebut juga intercept, sedangkan pada indeks sisanya merupakan koefisien beta untuk untuk masing-masing kolom
Penjelasan tentang fungsi tersebut akan dibahas pada perhitungan dibawah (poin 2a dan 2b)
Dim koefisienBeta() As Double = HitungKoefisienBeta(contohData)
2a. Tentukan matriks X dan matriks Y untuk digunakan dalam perhitungan koefisien Beta
Matriks X adalah semua data pada semua kolom kriteria selain kriteria hasil
Matriks Y adalah semua data pada kolom kriteria hasil saja
Langkah ini tidak wajib, hanya untuk memepermudah penjelasan rumus pada poin 2b.
Dim jumlahBaris As Integer = contohData.Length
Dim jumlahKolom As Integer = contohData(0).Length
Dim X(jumlahBaris - 1)() As Double
For i As Integer = 0 To jumlahBaris - 1
X(i) = New Double(jumlahKolom - 2) {}
Next i
Dim Y(jumlahBaris - 1)() As Double
For i As Integer = 0 To jumlahBaris - 1
Y(i) = New Double(0) {}
Next i
Dim j As Integer
For i As Integer = 0 To jumlahBaris - 1
For j = 0 To jumlahKolom - 2
X(i)(j) = contohData(i)(j)
Next j
Y(i)(0) = contohData(i)(j)
Next i
2b. Hitung Koefisien Beta dengan rumus
B = inv(Xt * X) * Xt * y
B adalah nilai koefisien beta yang akan dicari
X adalah semua data pada semua kolom kriteria selain kriteria hasil
Y adalah semua data pada kolom kriteria hasil saja
Xt adalah transpos matriks dari matriks X
inv adalah invers matriks dari matriks input
Dim Xt()() As Double = hitungTransposMatriks(X) Dim XtX()() As Double = hitungPerkalianMatriks(Xt, X) Dim inv()() As Double = hitungInversMatriks(XtX) Dim invXt()() As Double = hitungPerkalianMatriks(inv, Xt) Dim invXtY()() As Double = hitungPerkalianMatriks(invXt, Y)
2b1. Gunakan fungsi ini untuk menghitung transpos matriks
Private Function hitungTransposMatriks(ByVal matriks()() As Double) As Double()()
Dim jumlahBaris As Integer = matriks.Length
Dim jumlahKolom As Integer = matriks(0).Length
Dim hasil(jumlahKolom - 1)() As Double
For i As Integer = 0 To jumlahKolom - 1
hasil(i) = New Double(jumlahBaris - 1) {}
Next i
For i As Integer = 0 To jumlahBaris - 1
For j As Integer = 0 To jumlahKolom - 1
hasil(j)(i) = matriks(i)(j)
Next j
Next i
Return hasil
End Function
2b2. Gunakan fungsi ini untuk menghitung perkalian matriks
Private Function hitungPerkalianMatriks(ByVal matriksA()() As Double, ByVal matriksB()() As Double) As Double()()
Dim ajumlahBaris As Integer = matriksA.Length
Dim ajumlahKolom As Integer = matriksA(0).Length
Dim bjumlahBaris As Integer = matriksB.Length
Dim bjumlahKolom As Integer = matriksB(0).Length
If ajumlahKolom <> bjumlahBaris Then
Throw New Exception("Pada fungsi hitungPerkalianMatriks, Ukuran Matriks A dan B tidak sama")
End If
Dim hasil(ajumlahBaris - 1)() As Double
For i As Integer = 0 To ajumlahBaris - 1
hasil(i) = New Double(bjumlahKolom - 1) {}
Next i
For i As Integer = 0 To ajumlahBaris - 1
For j As Integer = 0 To bjumlahKolom - 1
For k As Integer = 0 To ajumlahKolom - 1
hasil(i)(j) += matriksA(i)(k) * matriksB(k)(j)
Next k
Next j
Next i
Return hasil
End Function
2b3. Gunakan fungsi ini untuk menghitung invers matriks
Private Function hitungInversMatriks(ByVal matriks()() As Double) As Double()()
Dim n As Integer = matriks.Length
'Salin Matriks
Dim hasil(n - 1)() As Double
For i = 0 To n - 1
hasil(i) = New Double(matriks(0).Length - 1) {}
For j = 0 To matriks(0).Length - 1
hasil(i)(j) = matriks(i)(j)
Next j
Next i
Dim permutasi() As Integer = Nothing
Dim matriksLU()() As Double = hitungDekomposisiMatriks(matriks, permutasi)
If matriksLU Is Nothing Then
Throw New Exception("Pada fungsi hitungInversMatriks, tidak dapat menghitung invers dari matriks")
End If
Dim b(n - 1) As Double
For i As Integer = 0 To n - 1
For j As Integer = 0 To n - 1
If i = permutasi(j) Then
b(j) = 1.0
Else
b(j) = 0.0
End If
Next j
Dim x() As Double = hitungPersamaanAxB(matriksLU, b)
For j As Integer = 0 To n - 1
hasil(j)(i) = x(j)
Next j
Next i
Return hasil
End Function
* Gunakan fungsi ini untuk menghitung dekomposisi matriks
Metode yang digunakan untuk mendekomposisi matriks adalah metode Dolittle
Private Function hitungDekomposisiMatriks(ByVal matriks()() As Double, <system.runtime.interopservices.out()> ByRef permutasi() As Integer) As Double()()
If matriks.Length <> matriks(0).Length Then
Throw New Exception("Pada fungsi hitungDekomposisiMatriks, ukuran baris dan kolom Matriks harus sama.")
End If
Dim n As Integer = matriks.Length
'Salin Matriks
Dim hasil(n - 1)() As Double
For i = 0 To n - 1
hasil(i) = New Double(matriks(0).Length - 1) {}
For j = 0 To matriks(0).Length - 1
hasil(i)(j) = matriks(i)(j)
Next j
Next i
permutasi = New Integer(n - 1) {}
For i As Integer = 0 To n - 1
permutasi(i) = i
Next i
For j As Integer = 0 To n - 2
Dim nilaiMaksimalBaris As Double = Math.Abs(hasil(j)(j)) ' nilai terbesar pada baris tersebut
'Cari Pivot
Dim barisPivot As Integer = j
For i As Integer = j + 1 To n - 1
If Math.Abs(hasil(i)(j)) > nilaiMaksimalBaris Then
nilaiMaksimalBaris = Math.Abs(hasil(i)(j))
barisPivot = i
End If
Next i
' Jika nilai terbesar tidak berada di pivot, tukar baris tersebut dengan baris sekarang
' dan tukar baris yang sama pada matriks permutasi
If barisPivot <> j Then
Dim rowPtr() As Double = hasil(barisPivot)
hasil(barisPivot) = hasil(j)
hasil(j) = rowPtr
Dim tmp As Integer = permutasi(barisPivot)
permutasi(barisPivot) = permutasi(j)
permutasi(j) = tmp
End If
'Jika setelah penukaran baris, ternyata nilai diagonal ada yang 0,
'maka lakukan pencarian baris data yang diagonalnya tidak 0 antara baris ini sampai baris terakhir
'kemudian tukar baris tersebut dan baris sekarang
'dan tukar baris yang sama pada matriks permutasi
If hasil(j)(j) = 0.0 Then
Dim barisBaru As Integer = -1
For baris As Integer = j + 1 To n - 1
If hasil(baris)(j) <> 0.0 Then
barisBaru = baris
End If
Next baris
If barisBaru = -1 Then
Throw New Exception("Pada fungsi hitungDekomposisiMatriks, tidak dapat menggunakan metode Doolittle")
End If
Dim rowPtr() As Double = hasil(barisBaru)
hasil(barisBaru) = hasil(j)
hasil(j) = rowPtr
Dim tmp As Integer = permutasi(barisBaru)
permutasi(barisBaru) = permutasi(j)
permutasi(j) = tmp
End If
'Lakukan dekomposisi matriks untuk mendapatkan matriks LU
For i As Integer = j + 1 To n - 1
hasil(i)(j) /= hasil(j)(j)
For k As Integer = j + 1 To n - 1
hasil(i)(k) -= hasil(i)(j) * hasil(j)(k)
Next k
Next i
Next j
Return hasil
End Function
</system.runtime.interopservices.out()>
3. Hitung nilai R-squared atau disebut juga koefisien determinasi
Koefisien ini tidak berhubungan dengan perhitungan data secara langsung, hanya untuk membuktikan seberapa cocok nilai koefisien beta terhadap data awal
Semakin mendekati angka 1.00, berarti prediksi yang dilakukan akan semakin baik
Penjelasan tentang fungsi tersebut akan dibahas pada perhitungan dibawah (poin 3a sampai dengan 3c)
Dim R2 As Double = RSquared(data, koefisienBeta)
3a. Hitung rata-rata dari kriteria hasil, dalam kasus ini adalah unit terjual
Dim jumlahY As Double = 0.0 For i As Integer = 0 To jumlahBaris - 1 jumlahY += data(i)(jumlahKolom - 1) Next i Dim rata2Y As Double = jumlahY / jumlahBaris
3b. Lakukan perulangan pada masing-masing data
Hitung sigma1, yaitu sigma kuadrat selisih hasil data dan hasil perhitungan
Kemudian hitung sigma2, yaitu sigma kuadrat selisih hasil data dengan rata-rata dari kriteria hasil
For i As Integer = 0 To jumlahBaris - 1 hasilData = data(i)(jumlahKolom - 1) hasilPerhitungan = koefisienBeta(0) For j As Integer = 0 To jumlahKolom - 2 hasilPerhitungan += koefisienBeta(j + 1) * data(i)(j) Next j sigma1 += (hasilData - hasilPerhitungan) * (hasilData - hasilPerhitungan) sigma2 += (hasilData - rata2Y) * (hasilData - rata2Y) Next i
3c. Hitung nilai R-squared dengan rumus 1 – (sigma1 / sigma2)
Return 1.0 - (sigma1 / sigma2)
4. Lakukan perhitungan dari masing-masing data awal menggunakan matriks koefisien beta yang sudah ditemukan
Kemudian catat tingkat kecocokan perhitungan data dengan hasil awal pada data, untuk membandingkan apakah nilai R-squared sudah cocok pada contoh data
Dim jumlahBenar As Integer = 0, jumlahSalah As Integer = 0
For i As Integer = 0 To contohData.Length - 1
Console.Write("Motor " & Chr(i + 65) & " ")
Console.Write(contohData(i)(4).ToString.PadRight(24) & " ")
Dim y As Double = HitungUnitTerjual(contohData(i)(1), contohData(i)(2), contohData(i)(3), koefisienBeta)
Console.Write(y.ToString("F0").PadRight(32))
If Math.Round(y) = contohData(i)(4) Then
jumlahBenar += 1
Console.Write("Benar")
Else
jumlahSalah += 1
Console.Write("Salah")
End If
Console.WriteLine()
Next
5. Untuk masing-masing data baru, hitung perkiraan hasil unit terjual menggunakan koefisien beta yang sudah ditentukan
For i As Integer = 0 To dataBaru.Length - 1
Console.Write("Motor " & Chr(i + 65 + 4) & " ")
Console.Write(dataBaru(i)(0).ToString("N0").PadRight(11) & " ")
Console.Write(dataBaru(i)(1).ToString.PadRight(23) & " ")
Console.Write(dataBaru(i)(2).ToString.PadRight(4) & " ")
Dim y As Double = HitungUnitTerjual(dataBaru(i)(0), dataBaru(i)(1), dataBaru(i)(2), koefisienBeta)
Console.Write(y.ToString("F0"))
Console.WriteLine()
Next
Hasil akhir adalah: (klik untuk perbesar gambar)
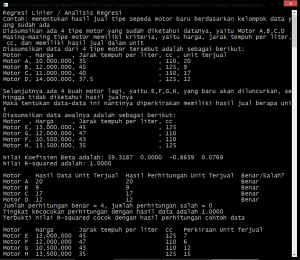
Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:
[sdm_download id=”838″ fancy=”0″]
Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.
