Algoritma Tabu Search 4

Algoritma ini adalah salah satu algoritma optimasi yang dapat digunakan untuk pengambilan keputusan. Contoh yang dibahas kali ini adalah mengenai pencarian posisi dengan pengembalian nilai fungsi maksimal.
Secara garis besar, langkah-langkah yang dilakukan algoritma ini adalah

• Tentukan posisi awal
• Tentukan semua titik disekitar titik tersebut
• Ambil titik terbaik
• Update daftar tabu
• Update indeks posisi
• Lakukan pencarian titik terbaik sampai memenuhi jumlah iterasi

Diasumsikan ada sebaran titik 2 dimensi antara -2 sampai dengan 2
Fungsi yang diketahui adalah fungsi Himmelblau, dengan rumus f(x, y) = (x^2+y-11)^2 + (x+y^2-7)^2
Tentukan posisi dimana fungsi tersebut mengembalikan nilai maksimal

Fungsi Himmelblau adalah salah satu fungsi yang dapat digunakan untuk mengoptimasi suatu permasalahan. Fungsi ini memiliki sebuah nilai maksimum pada x = -0.270845, and y = -0.923039 dengan nilai fungsi sebesar f(x,y) = 181.617, dengan asumsi bahwa rentang minimal dan maksimal dari sebaran titik adalah -2 sampai dengan 2

Grafik fungsi Himmelblau yang normal, atau untuk sebaran titik tak terbatas adalah sebagai berikut.

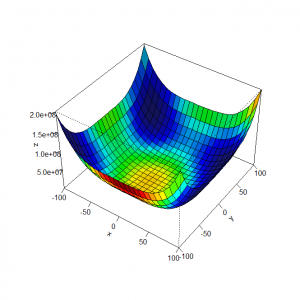
Sedangkan Grafik fungsi Himmelblau untuk sebaran titik dengan rentang minimal -2 dan maksimal 2 adalah sebagai berikut.

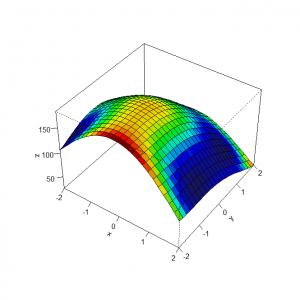
Dapat dilihat bahwa pada gambar tersebut, didapatkan area dengan titik tertinggi (berwarna merah) berada pada area x = -0, and y = -1, dimana titik tersebut mengembalikan nilai fungsi tertinggi. Oleh sebab itu digunakan algoritma ini untuk mencari titik di area berwarna merah tersebut.

Sebelum masuk kedalam langkah-langkah pembahasan algoritma, ada beberapa konstanta atau parameter yang harus diketahui, yaitu:
* Tentukan ukuran maksimal dari daftar tabu yang ada
Jika daftar tabu sudah penuh dengan data,
maka data berikutnya yang masuk daftar tabu akan menggantikan data yang pertama kali masuk ke dalam daftar tabu
Diasumsikan dalam kasus ini, ukuran maksimal daftar tabu adalah 20

Const ukuranDaftarTabu As Integer = 20

* Tentukan jumlah iterasi yang digunakan dalam perhitungan
Diasumsikan dalam kasus ini, jumlah iterasi adalah 50 kali

Const jumlahIterasi As Integer = 50

* Tentukan posisi minimal dan maksimal dari fungsi yang akan dihitung
Jika tidak ada batasan posisi, tentu saja posisi yang mendekati tak terhingga akan terpilih karena akan mengembalikan nilai fungsi yang sangat besar
Diasumsikan dalam kasus ini, posisi minimal adalah -2, dan posisi maksimal adalah +2

Const minPosisi As Double = -2
Const maksPosisi As Double = +2

Langkah-langkah penggunaan algoritma ini adalah

1. Tentukan angka-angka koordinat X dan Y yang dipakai dalam perhitungan
Diasumsikan dalam kasus ini, semua angka di dalam batas posisi akan dipakai dengan jarak antar titik adalah 0.05

Dim daftarKoordinatX((maksPosisi - minPosisi) / 0.05) As Double
For i As Integer = 0 To daftarKoordinatX.Length - 1
	daftarKoordinatX(i) = minPosisi + i * 0.05
Next

Dim daftarKoordinatY((maksPosisi - minPosisi) / 0.05) As Double
For i As Integer = 0 To daftarKoordinatY.Length - 1
	daftarKoordinatY(i) = minPosisi + i * 0.05
Next

2. Masukkan semua kombinasi posisi yang ditemukan ke dalam variabel titik

Dim titik As Titik(,) = New Titik(daftarKoordinatX.Length, daftarKoordinatY.Length) {}
For i As Integer = 0 To daftarKoordinatX.Length - 1
	For j As Integer = 0 To daftarKoordinatY.Length - 1
		titik(j, i) = New Titik(daftarKoordinatX(i), daftarKoordinatY(j))
	Next
Next

* Agar dapat menjalankan skrip diatas, maka diperlukan sebuah Class Titik untuk menampung data posisi X, posisi Y dan nilai fungsi titik tersebut. Deklarasi Class Titik adalah sebagai berikut:

Public Class Titik
    Implements IComparable(Of Titik)

    Private m_x As Double
    Private m_y As Double
    Private nilaiFungsi As Double

    Public Sub New(x As Double, y As Double)
        m_x = x
        m_y = y
        nilaiFungsi = HitungNilaiFungsi(x, y)
    End Sub

    Public Sub New(x As Double, y As Double, Nilai As Double)
        m_x = x
        m_y = y
        nilaiFungsi = Nilai
    End Sub

    Public Property x() As Double
        Get
            Return m_x
        End Get
        Set(value As Double)
            m_x = value
        End Set
    End Property

    Public Property y() As Double
        Get
            Return m_y
        End Get
        Set(value As Double)
            m_y = value
        End Set
    End Property

    Public Property Nilai() As Double
        Get
            Return nilaiFungsi
        End Get
        Set(value As Double)
            nilaiFungsi = value
        End Set
    End Property
	
	. . .
End Class

* Gunakan fungsi ini untuk menghitung nilai fungsi dengan rumus:
f(x, y) = (x ^ 2 + y – 11) ^ 2 + (x + y ^ 2 – 7) ^ 2

Public Function HitungNilaiFungsi(x1 As Double, y As Double) As Double
	Dim hasil As Double = Math.Pow(x1 * x1 + y - 11, 2) + Math.Pow(x1 + y * y - 7, 2)
	Return hasil
End Function

3. Tentukan indeks acak sebagai posisi titik awal mula sebelum dilakukan perhitungan
Kemudian buat titik awal dengan posisi acak tersebut

Dim rnd As New Random(0)
Dim idxAcakX As Integer = rnd.Next(daftarKoordinatX.Length)
Dim idxAcakY As Integer = rnd.Next(daftarKoordinatY.Length)
Dim titikAwal As New Titik(daftarKoordinatX(idxAcakX), daftarKoordinatY(idxAcakY))

4. Buat daftar tabu dengan jumlah maksimal sebanyak variabel ukuran daftar tabu
Kemudian masukkan titik awal mula yang sudah ditemukan ke dalam daftar tabu tersebut

Dim daftarTabu As New DaftarTabu(Of Titik)(ukuranDaftarTabu)
daftarTabu.TambahTabu(titikAwal)

* Agar dapat menjalankan skrip diatas, maka diperlukan sebuah Class DaftarTabu untuk menampung data daftar titik tabu dan ukuran maksimal daftar tabu. Deklarasi Class DaftarTabu adalah sebagai berikut:

Public Class DaftarTabu(Of T)
    Private daftarTitikTabu As New Queue(Of Titik)()
    Private maksDaftarTabu As Integer

    Public Sub New(maksDaftarTabu As Integer)
        Me.maksDaftarTabu = maksDaftarTabu
    End Sub
	
	. . .
End Class

* Gunakan fungsi ini untuk menambahkan sebuah titik ke dalam daftar tabu

Public Sub TambahTabu(t As Titik)
	If daftarTitikTabu.Count() >= maksDaftarTabu Then daftarTitikTabu.Dequeue()
	daftarTitikTabu.Enqueue(t)
End Sub

5. Lakukan proses pencarian posisi terbaik sebanyak jumlah iterasi
Penjelasan lebih detail tentang fungsi ini dapat dilihat pada penjelasan skrip dibawah ini (poin 5a – 5c)

ts.CariPosisiTerbaik(titik, daftarTabu, daftarKoordinatX, daftarKoordinatY)

Memasuki perhitungan pada fungsi CariPosisiTerbaik

5a. Simpan semua titik disekitar parameter titik beserta nilai titik tersebut
Jika indeks yang dihitung menyebabkan titik berada diluar batas koordinat posisi, maka beri nilai titik dengan posisi (0, 0)

For i As Integer = -1 To 1
	For j As Integer = -1 To 1
		If Not ((i = 0) And (j = 0)) Then
			Try
				daftarTitikSekitar(idxDaftarTitikSekitar) = New Titik(titik(idxY + j, idxX + i).x, titik(idxY + j, idxX + i).y, titik(idxY + j, idxX + i).Nilai)
				idxDaftarTitikSekitar += 1
			Catch
				daftarTitikSekitar(idxDaftarTitikSekitar) = New Titik(0, 0, 0)
				idxDaftarTitikSekitar += 1
			End Try
		End If
	Next
Next

5b. Lakukan pengurutan titik dari nilai fungsi yang tertinggi ke nilai fungsi yang terendah

Array.Sort(daftarTitikSekitar)

5c. Lakukan perhitungan pada semua titik pada daftar tersebut (poin 5c1 – 5c4)

For Each t As Titik In daftarTitikSekitar
. . .

5c1. Lakukan perhitungan selanjutnya apabila titik yang sedang dihitung tidak termasuk dalam daftar tabu

If Not daftarTabu.isTerdapatDalamTabu(t) Then
. . .

* Gunakan fungsi ini untuk mengetahui apakah sebuah titik sudah masuk ke dalam daftar tabu
Fungsi ini akan mengembalikan nilai TRUE apabila titik tersebut terdapat dalam daftar tabu, selain itu akan mengembalikan nilai FALSE

Public Function isTerdapatDalamTabu(p As Titik) As Boolean
	Dim x = From t In daftarTitikTabu Where t.x = p.x AndAlso t.y = p.y AndAlso t.Nilai = p.Nilai Select t
	Return x.Count() > 0
End Function

5c2. Jika nilai fungsi pada titik ini lebih dari nilai fungsi titik terbaik,
Maka simpan titik ini sebagai titik terbaik
Dan tambakan titik ini kedalam daftar tabu

If t.Nilai > TitikTerbaik.Nilai Then
	TitikTerbaik = t
	daftarTabu.TambahTabu(t)
End If

5c3. Simpan indeks titik yang sedang dihitung pada posisi X dan Y

For i As Integer = 0 To daftarKoordinatX.Length - 1
	If t.x = daftarKoordinatX(i) Then
		idxX = i
		Exit For
	End If
Next

For i As Integer = 0 To daftarKoordinatY.Length - 1
	If t.y = daftarKoordinatY(i) Then
		idxY = i
		Exit For
	End If
Next

5c4. Jika iterasi masih belum melebihi jumlah maksimal iterasi
Maka ulangi fungsi ini kembali (poin 5) dengan posisi titik yang sedang dihitung
Jika iterasi sudah melebihi jumlah maksimal iterasi, maka hentikan perhitungan

If iterasi = jumlahIterasi Then
	Exit For
Else
	iterasi += 1
	CariPosisiTerbaik(titik, daftarTabu, daftarKoordinatX, daftarKoordinatY)
End If

* Agar dapat menjalankan skrip diatas, maka diperlukan sebuah Class TS untuk menampung data indeks koordinat X dan Y, jumlah iterasi, dan titik dengan nilai fungsi terbaik. Deklarasi Class TS adalah sebagai berikut:

Class TS
    Private idxX As Integer             'Indeks Koordinat X sebuah Titik pada data awal
    Private idxY As Integer             'Indeks Koordinat Y sebuah Titik pada data awal
    Private jumlahIterasi As Integer
    Private iterasi As Integer
    Private TitikTerbaik As Titik       ' variable of type Titik for storing the coordinates and value of global minimum

    Public Sub New(idxX As Integer, idxY As Integer, jumlahIterasi As Integer, titikAwal As Titik)
        Me.idxX = idxX
        Me.idxY = idxY
        Me.jumlahIterasi = jumlahIterasi
        iterasi = 1
        TitikTerbaik = titikAwal
    End Sub

    Public ReadOnly Property PosisiTerbaik As Titik
        Get
            Return TitikTerbaik
        End Get
    End Property

	. . .
End Class

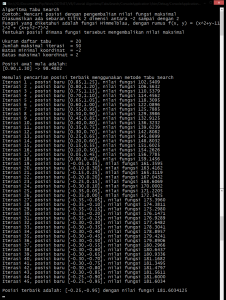
Hasil akhir adalah: (klik untuk perbesar gambar)

Dapat dilihat bahwa hasil akhir perhitungan tidak sama dengan x = -0.270845, and y = -0.923039, tetapi hanya mendekati posisi tersebut. Hal ini disebabkan karena semua posisi titik awal yang digunakan sudah dibulatkan menjadi 2 angka dibelakang koma.

Contoh modul / source code dalam bahasa VB (Visual Basic) dapat didownload disini:

Jika membutuhkan jasa kami dalam pembuatan program, keterangan selanjutnya dapat dilihat di Fasilitas dan Harga
Jika ada yang kurang paham dengan langkah-langkah algoritma diatas, silahkan berikan komentar Anda.
Selamat mencoba.